本题文科做.
已知二次函数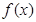
的二次项系数为
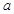，且不等式
的解集为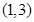
．
(1)若方程
有两个相等的实数根, 求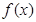的解析式；
(2)若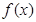的最大值为正数，求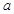的取值范围．
设函数
（1）求函数f(x)的单调区间，并求函数f(x)的极大值和极小值；
（2）当x∈[a+1, a+2]时，不等
，求a的取值范围.
已知函数f（x）＝ax2＋bx＋c，其中a∈N*，b∈N，c∈Z。
（1）若b>2a，且f（sinx）（x∈R）的最大值为2，最小值为－4，试求函数f（x）的最小值；
（2）若对任意实数x，不等式4x≤f（x）≤2（x2＋1）恒成立，且存在x0，使得f（x0）<2（x02＋1）成立，求c的值。
设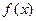
是定义域在
上的奇函数，且其图象上任意两点连线的斜率均小于零.
（l）求证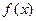在上是减函数；
（ll）如果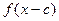
，
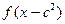的定义域的交集为空集，求实数
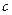的取值范围；
（lll）证明若
，则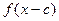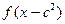，存在公共的定义域，并求这个公共的空义域.
已知函数f(x)=
，其中
（I）若b>2a,且 f(sinx)(x∈R)的最大值为2，最小值为－4，试求函数f(x)的最小值；
（II）若对任意实数x，不等式
恒成立,且存在
成立，求c的值。
二次函数f(x)=
（I）若方程f(x)=0无实数根，求证：b>0；
（II）若方程f(x)=0有两实数根，且两实根是相邻的两个整数，求证：f(－a)=
；
（III）若方程f(x)=0有两个非整数实根，且这两实数根在相邻两整数之间，试证明存在整数k，使得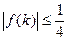
.