在数列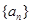 中,
中,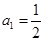 ,点
,点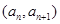 在直线
在直线 上.
上.
(Ⅰ)求数列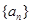 的通项公式;
的通项公式;
(Ⅱ)记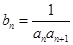 ,求数列
,求数列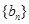 的前n项和
的前n项和 .
.
已知函数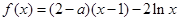 ,
, 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当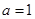 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)若函数 在
在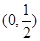 上无零点,求
上无零点,求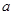 最小值;
最小值;
(Ⅲ)若对任意给定的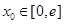 ,在
,在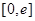 上总存在两个不同的
上总存在两个不同的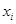
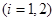 ),使
),使 成立,求
成立,求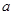 的取值范围.
的取值范围.
给定椭圆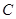 :
:
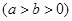 ,称圆心在原点
,称圆心在原点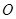 ,半径为
,半径为 的圆是椭圆
的圆是椭圆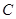 的“准圆”.若椭圆
的“准圆”.若椭圆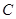 的一个焦点为
的一个焦点为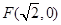 ,且其短轴上的一个端点到
,且其短轴上的一个端点到 的距离为
的距离为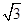 .
.
(Ⅰ)求椭圆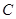 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(Ⅱ)点 是椭圆
是椭圆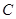 的“准圆”上的一个动点,过动点
的“准圆”上的一个动点,过动点 作直线
作直线 ,使得
,使得 与椭圆
与椭圆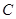 都只有一个交点,试判断
都只有一个交点,试判断 是否垂直,并说明理由.
是否垂直,并说明理由.
如图,四棱锥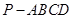 中,
中,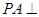 底面
底面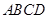 ,四边形
,四边形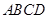 中,
中, ,
,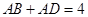 ,
,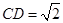 ,
, .
.
(Ⅰ)求证:平面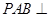 平面
平面 ;
;
(Ⅱ)设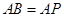 .
.
(ⅰ) 若直线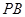 与平面
与平面 所成的角为
所成的角为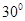 ,求线段
,求线段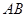 的长;
的长;
(ⅱ) 在线段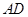 上是否存在一个点
上是否存在一个点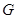 ,使得点
,使得点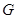 到点
到点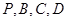 的距离都相等?说明理由.
的距离都相等?说明理由.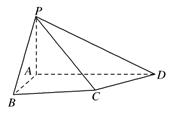
(本小题满分12分)等差数列 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为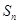 ,等比数列
,等比数列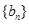 中,
中,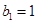 ,
,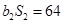 ,
,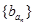 是公比为64的等比数列.
是公比为64的等比数列.
(Ⅰ)求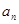 与
与 ;
;
(Ⅱ)证明: .
.