已知函数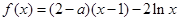 ,
, 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当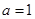 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ)若函数 在
在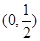 上无零点,求
上无零点,求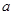 最小值;
最小值;
(Ⅲ)若对任意给定的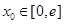 ,在
,在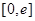 上总存在两个不同的
上总存在两个不同的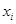
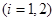 ),使
),使 成立,求
成立,求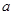 的取值范围.
的取值范围.
(本题满分14分,第1小题6分,第2小题8分)
在正方体 中,
中, 是棱
是棱 的中点.
的中点.
(1)求直线 与平面
与平面 所成角的大小(结果用反三角函数表示)
所成角的大小(结果用反三角函数表示)
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若存在,指明点
,若存在,指明点 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
已知函数 ,
, .
.
(1)若直线 是函数
是函数 的图像的一条对称轴,求
的图像的一条对称轴,求 的值;
的值;
(2)若 ,求
,求 的值域.
的值域.
已知函数 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的图象在点
的图象在点 处的切线方程;
处的切线方程;
(Ⅱ)当 时,记函数
时,记函数 ,试求
,试求 的单调递减区间;
的单调递减区间;
(Ⅲ)设函数 (其中
(其中 为常数),若函数
为常数),若函数 在区间
在区间 上不存在极值,求
上不存在极值,求 的最大值.
的最大值.
已知抛物线
 的焦点为
的焦点为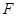 ,抛物线上存在一点
,抛物线上存在一点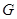 到焦点的距离为
到焦点的距离为 ,且点
,且点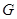 在圆
在圆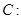
 上.
上.
(Ⅰ)求抛物线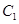 的方程;
的方程;
(Ⅱ)已知椭圆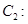
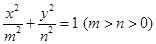 的一个焦点与抛物线
的一个焦点与抛物线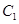 的焦点重合,且离心率为
的焦点重合,且离心率为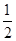 .直线
.直线 交椭圆
交椭圆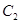 于
于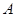 、
、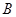 两个不同的点,若原点
两个不同的点,若原点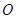 在以线段
在以线段 为直径的圆的外部,求
为直径的圆的外部,求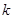 的取值范围.
的取值范围.
如图,在正四棱台 中,
中, ,
,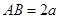 ,
, ,
, 、
、 分别是
分别是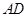 、
、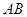 的中点.
的中点. 
(Ⅰ)求证:平面 ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 .
.
注:底面为正方形,从顶点向底面作垂线,垂足是底面中心,这样的四棱锥叫做正四棱锥.用一个平行于正四棱锥底面的平面去截该棱锥,底面与截面之间的部分叫做正四棱台.