如图,有四条互相不平行的直线L1、L2、L3、L4所截出的八个角.请你任意选择其中的三个角(不可选择未标注的角),尝试找到它们的关系,并选择其中一组予以证明. 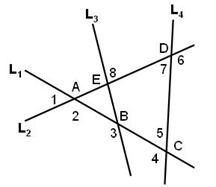
画一画:已知:如图△ABC.试作△ABC的:①中线AD;②角平分线BE;③高线CH.
如图,是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2),(2,3).完成以下问题: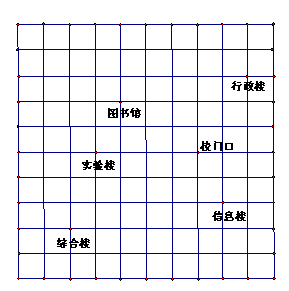
请根据题意在图上建立直角坐标系;
写出图上其他地点的坐标
在图中用点P表示体育馆(-1,-3)的位置
如图,已知AB//CD,猜想图1、图2、图3中∠B,∠BED,∠D之间有什么关系?请用等式表示出它们的关系。并证明其中的一个等式。(本题9分)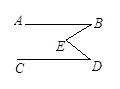
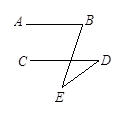
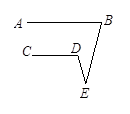
图1图2图3
1.2.3.
下面是我国几个城市今年三月份的平均降水量。(本题4分)
| 地区 |
昆明 |
广州 |
海口 |
上海 |
| 降水量(毫升) |
11 |
33 |
22 |
44 |
你能制作形象的统计图表示这几个地区三月份的平均降水量吗甲、乙两人打赌,甲说,往图中的区域掷石子,它一定会落在阴影部分上,乙说决不会落在阴影部分上,你认为谁获胜的概率较大?通过计算说明.

如右图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA. 
证明:∵AD⊥BC,EF⊥BC ( )
∴∠EFB=∠ADB=90° ( )
∴EF∥AD( )
∴∠1=∠BAD ( )
又∵∠1=∠2 ( )
∴(等量代换)
∴DG∥BA.( )