如图,已知△ABC中,AB="AC=6" cm, ,BC="4" cm,点D为AB的中点
,BC="4" cm,点D为AB的中点如果点P在线段BC上以1 cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,
请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使
△BPD与△CQP全等?若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

某中学为了解该校学生一年的课外阅读量,随机抽取了 名学生进行调查,并将调查结果绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
(1)求 的值;
(2)根据统计结果,估计该校1100名学生中一年的课外阅读量超过10本的人数.

、 两种型号的机器加工同一种零件,已知 型机器比 型机器每小时多加工20个零件, 型机器加工400个零件所用时间与 型机器加工300个零件所用时间相同,求 型机器每小时加工零件的个数.
一个不透明的口袋中有三个小球,上面分别标有数字0,1,2,每个小球除数字不同外其余均相同,小华先从口袋中随机摸出一个小球,记下数字后放回并搅匀;再从口袋中随机摸出一个小球记下数字、用画树状图(或列表)的方法,求小华两次摸出的小球上的数字之和是3的概率.
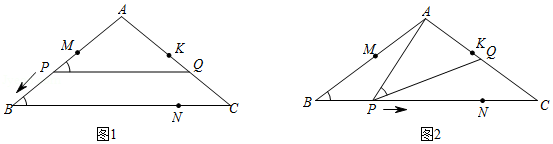
如图1和图2,在 中, , , .点 在 边上,点 , 分别在 , 上,且 .点 从点 出发沿折线 匀速移动,到达点 时停止;而点 在 边上随 移动,且始终保持 .
(1)当点 在 上时,求点 与点 的最短距离;
(2)若点 在 上,且 将 的面积分成上下 两部分时,求 的长;
(3)设点 移动的路程为 ,当 及 时,分别求点 到直线 的距离(用含 的式子表示);
(4)在点 处设计并安装一扫描器,按定角 扫描 区域(含边界),扫描器随点 从 到 再到 共用时36秒.若 ,请直接写出点 被扫描到的总时长.
如图,甲、乙两人(看成点)分别在数轴 和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率 ;
(2)从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对 次,且他最终停留的位置对应的数为 ,试用含 的代数式表示 ,并求该位置距离原点 最近时 的值;
(3)从如图的位置开始,若进行了 次移动游戏后,甲与乙的位置相距2个单位,直接写出 的值.
