某商场用36万元购进A、B两种商品，销售完后共获利6万元，其进价和售价如下表：
| |
A |
B |
| 进价（元/件） |
1200 |
1000 |
| 售价（元/件） |
1380 |
1200 |
（注：获利 = 售价 — 进价）该商场购进A、B两种商品各多少件；
商场第二次以原进价购进A、B两种商品．购进B种商品的件数不变，而购进A种商品的件数是第一次的2倍，A种商品按原售价出售，而B种商品打折销售．若两种商品销售完毕，要使第二次经营活动获利不少于81600元，B种商品最低售价为每件多少元？
如图，抛物线F：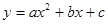
的顶点为P，抛物线：与y轴交于点A，与直线OP交于点B．过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得到抛物线F′：
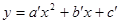，抛物线F′与x轴的另一个交点为C．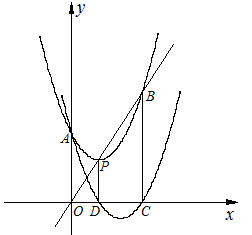
⑴当a = 1，b=－2，c = 3时，求点C的坐标(直接写出答案)；
⑵若a、b、c满足了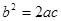
①求b：b′的值；
②探究四边形OABC的形状，并说明理由．
如图15，在△ABC和△PQD中，AC =" k" BC，DP =" k" DQ，∠C =∠PDQ，D、E分别是AB、AC的中点，点P在直线BC上，连结EQ交PC于点H．猜想线段EH与AC的数量关系，并证明你的猜想．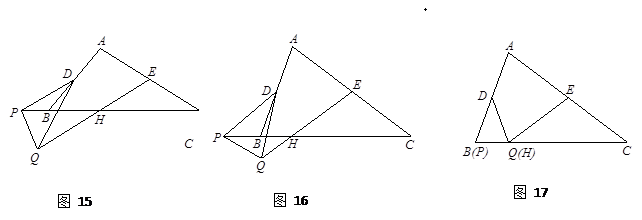
如图14，矩形ABCD中，AB = 6cm，AD = 3cm，点E在边DC上，且DE = 4cm．动点P从点A开始沿着A→B→C→E的路线以2cm/s的速度移动，动点Q从点A开始沿着AE以1cm/s的速度移动，当点Q移动到点E时，点P停止移动．若点P、Q同时从点A同时出发，设点Q移动时间为t (s)，P、Q两点运动路线与线段PQ围成的图形面积为S (cm2)，求S与t的函数关系式．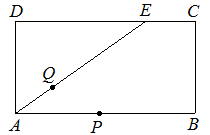
A、B两地的路程为16千米，往返于两地的公交车单程运行40分钟．某日甲车比乙车早20分钟从A地出发，到达B地后立即返回，乙车出发20分钟后因故停车10分钟，随后按原速继续行驶，并与返回途中的甲车相遇．图13是乙车距A地的路程y (千米)与所用时间x (分)的函数图象的一部分(假设两车都匀速行驶)．
⑴请在图13中画出甲车在这次往返中，距A地的路程y (千米)与时间x (分)的函数图象；
⑵乙车出发多长时间两车相遇？
如图，直线
交x轴于点A，交y轴于点B，抛物线
的顶点为A，且经过点B．
⑴求该抛物线的解析式；
⑵若点C(m，
)在抛物线上，求m的值．