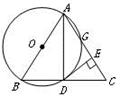
已知,AB为⊙O 的直径,点E 为弧AB 任意一点,如图,AC平分∠BAE,交⊙O于C ,过点C作CD⊥AE于D,与AB的延长线交于P.
⑴求证:PC是⊙O的切线.⑵若∠BAE=60°,求线段PB与AB的数量关系.
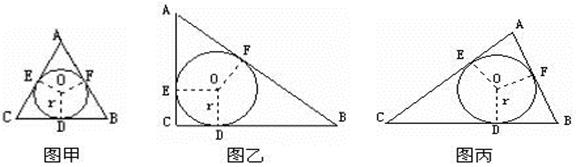
为了探究三角形的内切圆半径r与周长 、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
、面积S之间的关系,在数学实验活动中,选取等边三角形(图甲)和直角三角形(图乙)进行研究.⊙O是△ABC的内切圆,切点分别为点D、E、F.
(1)用刻度尺分别量出表中未度量的△ABC的长,填入空格处,并计算出周长 和面积S.(结果精确到0.1厘米)
和面积S.(结果精确到0.1厘米)
| |
AC |
BC |
AB |
r |
 |
S |
| 图甲 |
|
|
|
0.6 |
|
|
| 图乙 |
|
|
|
1.0 |
|
|
(2)观察图形,利用上表实验数据分析.猜测特殊三角形的r与 、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
、S之间关系,并证明这种关系对任意三角形(图丙)是否也成立?
(3) 
已知:如图,⊙O1与坐标轴交于A(1,0)、B(5,0)两点,点O1的纵坐标为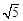 .求⊙O1的半径.
.求⊙O1的半径.
已知:如图, 为
为 的直径,
的直径,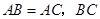 交
交 于点
于点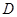 ,
, 交
交 于点
于点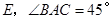 .
.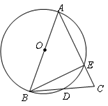
(1)求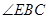 的度数;
的度数;
(2)求证: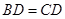 .
.
如图,以等腰三角形 的一腰
的一腰 为直径的⊙O交底边
为直径的⊙O交底边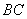 于点
于点 ,交
,交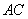 于点
于点 ,连结
,连结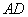 ,并过点
,并过点 作
作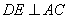 ,垂足为
,垂足为 .根据以上条件写出三个正确结论(除
.根据以上条件写出三个正确结论(除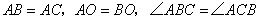 外)是:
外)是:
(1)________________;(2)________________;(3)________________.