如图1,梯形 中,
中, ∥
∥ ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形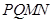 ,点
,点 在射线
在射线 上,当
上,当 点到达
点到达 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
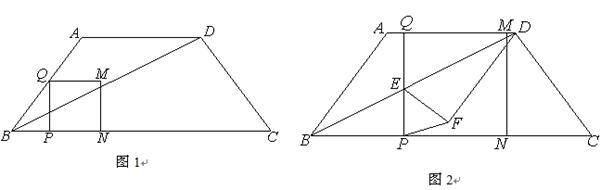
的运动时间为 秒(
秒( ).
).
(1)当正方形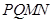 的边
的边 恰好经过点
恰好经过点 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设正方形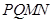 与△
与△ 的重合部分面积为
的重合部分面积为 ,请直接写
,请直接写
出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图2,当点 在线段
在线段 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△
沿 翻折,得到△
翻折,得到△ ,连接
,连接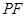 .是否存在这样的
.是否存在这样的 ,使△
,使△ 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,在平面直角坐标系中, OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数
OABC的顶点A, C的坐标分别为A(2,0),C(-1,2),反比例函数 的图像经过点B.
的图像经过点B.
(1)求k的值.
(2)将 OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数
OABC沿着x轴翻折,点C落在点C′处.判断点C′是否在反比例函数 的图像上,请通过计算说明理由.
的图像上,请通过计算说明理由.
图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个四边形ABCD.
要求:四边形ABCD的顶点D在格点上,且有两个角相等(一组或两组角相等均可);所画的两个四边形不全等.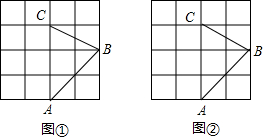
如图,有一个晾衣架放置在水平地面上,在其示意图中,支架OA、OB的长均为108cm,支架OA与水平晾衣杆OC的夹角∠AOC为59°,求支架两个着地点之间的距离AB.(结果精确到0.1cm)(参考数据:sin59°=0.86,cos59°=0.52,tan59°=1.66).
长春市某校准备组织七年级学生游园,供学生选择的游园地点有:东北虎园、净月潭、长影世纪城,每名学生只能选择其中一个地点.该校学生会从七年级学生中随机抽取了a名学生,对他们选择各游园点的情况进行了调查,并根据调查结果绘制成如下条形统计图.
(1)求a的值.
(2)求这a名学生选择去净月潭游园的人数的百分比.
(3)按上述调查结果,估计该校七年级650名学生中选择去净月潭游园的人数.
如图,在同一平面内,有一组平行线l1、l2、l3,相邻两条平行线之间的距离均为4,点O在直线l1上,⊙O与直线l3的交点为A、B,AB=12,求⊙O的半径.