附加题(按满分5分计入总分,若总分超过满分值以满分计算)
如果集合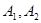 满足
满足 ,则称(
,则称(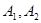 )为集合
)为集合 的一种分拆.并规定:当且仅当
的一种分拆.并规定:当且仅当 时,(
时,(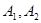 )与(
)与(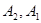 )为集合
)为集合 的同一种分拆.请计算集合
的同一种分拆.请计算集合 所有不同的分拆种数有多少种?
所有不同的分拆种数有多少种?
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2. 
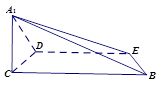
图1图2
(1)求证:A1C⊥平面BCDE;
(2)过点E作截面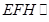 平面
平面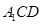 ,分别交CB于F,
,分别交CB于F,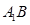 于H,求截面
于H,求截面 的面积;
的面积;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE成 的角?说明理由.
的角?说明理由.
如图,已知二面角α—AB—β的大小为120º,PC⊥α于C,PD⊥β于D,且PC=2,PD=3.
(1)求异面直线AB与CD所成角的大小;
(2)求点P到直线AB的距离.
如图,正方体ABCD—A1B1C1D1棱长为8,E、F分别为AD1,CD1中点,G、H分别为棱DA,DC上动点,且EH⊥FG.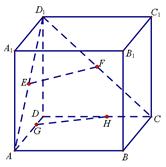
(1)求GH长的取值范围;
(2)当GH取得最小值时,求证:EH与FG共面;并求出此时EH与FG的交点P到直线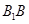 的距离.
的距离.
如图,空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,且AB=AD,BC=DC.
(1)求证: 平面EFGH;
平面EFGH;
(2)求证:四边形EFGH是矩形.
如图,正方体ABCD—A1B1C1D1中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.