(本小题满分13分)
高三年级进行模拟考试,某班参加考试的40名同学的成绩统计如下:
| 分数段 |
(70,90) |
[90,100) |
[100,120) |
[120,150] |
| 人数 |
5 |
a |
15 |
b |
规定分数在90分及以上为及格,120分及以上为优秀,成绩高于85分低于90分的同学为希望生.已知该班希望生有2名.
(Ⅰ)从该班所有学生中任选一名,求其成绩及格的概率;
(Ⅱ)当a =11时,从该班所有学生中任选一名,求其成绩优秀的概率;
(Ⅲ)从分数在(70,90)的5名学生中,任选2名同学参加辅导,求其中恰有1名希望生的概率.
如图,在四棱锥 中,底面
中,底面 是矩形,
是矩形,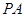 ⊥平面
⊥平面 ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
(1)证明: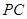 ⊥平面
⊥平面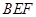 ;
;
(2)求平面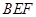 与平面
与平面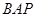 夹角的大小.
夹角的大小. 
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖.某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值 元的概率分布列.
元的概率分布列.
已知 为
为 的三个内角,其所对的边分别为
的三个内角,其所对的边分别为 ,且
,且 .
.
(1)求角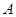 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.
等差数列 中,
中,
(1)求 的通项公式;
的通项公式;
(2)设
已知函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)若函数 在区间
在区间 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;
(3)当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.