(本小题满分13分)
一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.
(Ⅰ)求取出的3个球颜色相同且编号是三个连续整数的概率;
(Ⅱ)求取出的3个球中恰有2个球编号相同的概率;
(Ⅲ)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.
在正方体ABCD—A1B1C1D1中
(1)求证: BD⊥平面ACC1
(2)求二面角C1—BD—C的正切值
 |
一用户到电信局打算上网开户,经询问,有三种月消费方式:(1)163普通方式:上网资费2元/小时;(2)163A方式:每月30元(可上网50小时),超过50小时以上的资费为 2元/小时;(3) ADLSD方式:每月50元,时长不限(其它因素均忽略不计)。(每月以30日计算)
(1)、分别写出三种上网方式中所用月资费( )与时间(
)与时间(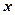 )的函数关系式;
)的函数关系式;
(2)、在同一坐标系内画出三种上网方式中所用资费与时间的函数图象;
(3)、根据你的研究,给这一用户一个合理化的建议。
已知圆的方程为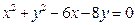 .圆内一点P
.圆内一点P
(1).若EF为过点P且倾斜角 =1350的弦,求EF的长;
=1350的弦,求EF的长;
(2).若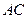 和
和 分别为过P
分别为过P 的最长弦和最短弦,求四边形
的最长弦和最短弦,求四边形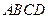 的面积。
的面积。
已知圆M:x2+y2-4y+3=0, Q是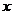 轴上的动点,QA、QB分别切圆M
轴上的动点,QA、QB分别切圆M
于A、B两点,(1)如果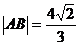 ,求点Q的坐标及直线MQ的方程;
,求点Q的坐标及直线MQ的方程;
(2)求动弦∣AB∣的最小值。
如图,在四面体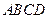 中,
中,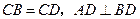 ,点
,点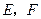 分别是
分别是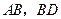 的中点.
的中点.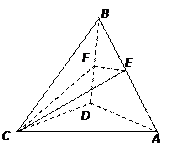
求证:(1)直线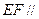 面
面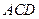 ;
;
(2)平面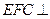 面
面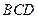 .
.