第26届世界大学生夏季运动会将于2011年11月12日到23日在深圳举行 ,为了搞好接待工作,组委会在某学院招募了12名男志愿者和18名女志愿者。将这30名志愿者的身高编成如右所示的茎叶图(单位:cm):若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”。
(1)如果用分层抽样的方法从“高个子”和“非高个子”中中提取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少?
(2)若从所有“高个子”中选3名志愿者,用 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。
已知函数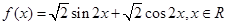 .
.
(1)求 的最大值和最小正周期;
的最大值和最小正周期;
(2)若 ,
,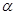 是第二象限的角,求
是第二象限的角,求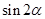 .
.
(本小题满分14分)如图,已知圆E: ,点
,点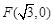 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(Ⅰ)求动点Q的轨迹 的方程;
的方程;
(Ⅱ)设直线 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹 相交于
相交于 两点,直线
两点,直线 的斜率分别为
的斜率分别为
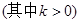 .△
.△ 的面积为
的面积为 ,以
,以 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若 恰好构成等比数列,求
恰好构成等比数列,求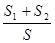 的取值范围.
的取值范围.
(本小题满分14分)某创业投资公司拟投资开发某种新能源产品,估计能获得投资收益的范围是 (单位:万元).现准备制定一个对科研课题组的奖励方案:奖金
(单位:万元).现准备制定一个对科研课题组的奖励方案:奖金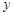 (单位:万元)随投资收益
(单位:万元)随投资收益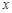 (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过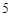 万元,同时奖金不超过投资收益的20%.
万元,同时奖金不超过投资收益的20%.
(Ⅰ)若建立函数模型 制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
(Ⅱ)现有两个奖励函数模型: ;
;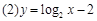 .试分析这两个函数模型是否符合公司要求.
.试分析这两个函数模型是否符合公司要求.
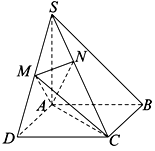
(本小题满分13分)如图,在四棱锥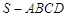 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, , 点
, 点 是
是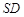 的中点,
的中点, ,且交
,且交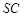 于点
于点 .
.
(Ⅰ)求证: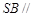 平面
平面 ;
;
(Ⅱ)求证:直线 平面
平面 ;
;
(Ⅲ)求直线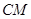 与平面
与平面 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)已知等比数列 满足:
满足: ,且
,且 是
是 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列{an}是单调递增的,令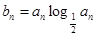 ,
, ,求使
,求使 成立的正整数
成立的正整数 的最小值.
的最小值.