某小区要建一个面积为500平方米的矩形绿地,四周有小路,绿地长边外路宽5米,短边外路宽9米,怎样设计绿地的长与宽,使绿地和小路所占的总面积最小,并求出最小值。
(本小题满分12分)
在极坐标系中,已知圆C的圆心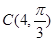 ,半径r=2,Q点在圆C上运动。
,半径r=2,Q点在圆C上运动。
(I)求圆C的极坐标方程;
(II)若P在直线OQ上运动,且OQ∶OP=3∶2,求动点P的轨迹方程。
(本小题满分12分)已知点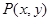 是圆
是圆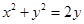 上的动点,
上的动点,
(1)求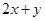 的取值范围;
的取值范围;
(2)若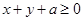 恒成立,求实数
恒成立,求实数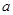 的取值范围。
的取值范围。
(本小题满分12分)
若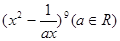 的展开式中
的展开式中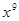 的系数是
的系数是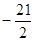 .
.
(1)求展开式中的常数项;
(2)求 的值.
的值.
已知等差数列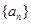 的前
的前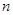 项和为
项和为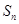 ,且
,且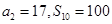 .
.
(I)求数列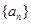 的通项公式;
的通项公式;
(II)若数列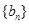 满足
满足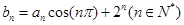 ,求数列
,求数列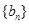 的前
的前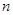 项和.
项和.
某小区要建一座八边形的休闲小区,如右图它在主体造型的平面图是由两个相同的矩形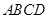 和
和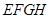 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
⑴设总造价为 元,
元, 长为
长为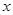 米,试求
米,试求 关于
关于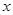 的函数关系式;
的函数关系式;
⑵当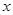 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值.