求证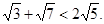
如图，已知C、F是以AB为直径的半圆
上的两点，且CF＝CB，过C作CD^AF交AF的延长线与点D．
(Ⅰ)证明：CD为圆O的切线；
(Ⅱ)若AD＝3，AB＝4，求AC的长．
已知函数f (x)＝－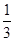
ax3＋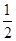
x2＋(a－1)x－
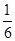(x＞0)，(aÎR)．
(Ⅰ)当0＜a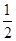＜时，讨论f (x)的单调性；
(Ⅱ)若f (x)在区间(a, a＋1)上不具有单调性，求正实数a的取值范围．
已知中心在原点O，焦点在x轴上的椭圆E过点(1，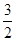
)，离心率为
．
(Ⅰ)求椭圆E的方程；
(Ⅱ)直线x＋y＋1＝0与椭圆E相交于A、B(B在A上方)两点，问是否存在直线l，使l与椭圆相交于C、D(C在D上方)两点且ABCD为平行四边形，若存在，求直线l的方程与平行四边形ABCD的面积；若不存在，请说明理由．
如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC＝90°，AB＝2，点D1、D分别是棱B1C1、BC的中点．
(Ⅰ)求证：A1D1⊥平面BB1C1C；
(Ⅱ)求证：AB1∥平面CA1D1；
（Ⅲ）求多面体A1B1D1-CAD的体积．
甲､乙两名运动员在一次射击预选赛中，分别射击了4次，成绩如下表（单位：环）：
| 甲 |
6 |
7 |
9 |
10 |
| 乙 |
6 |
8 |
8 |
10 |
(Ⅰ)从甲､乙两人的成绩中各随机抽取一个，求甲的成绩比乙高的概率；
(Ⅱ)现要从中选派一人参加正式比赛，你认为选派哪位运动员参加比较合适?请说明理由．