将正方形ABCD绕中心O顺时针旋转角
得到正方形
，如图1所示.当
=45
时(如图2)，若线段
与边
的交点为
，线段
与
的交点为
，可得下列结论成立 ①
；②
，试选择一个证明.当
时,第（1）小题中的结论还成立吗?如果成立，请证明;如果不成立，请说明理由在旋转过程中，记正方形
与AB边相交于P,Q两点，探究
的度数是否发生变化？如果变化，请描述它与之间的关系;如果不变，请直接写出的度数.
如图，
点
在
轴的正半轴上，
，
，
．点
从点
出发，沿
轴向左以每秒1个单位长的速度运动，运动时间为
秒．
（1）点的坐标是 ；
（2）当
时，求的值；
（3）以点为圆心，
为半径的
随点的运动而变化，当与四边形
的边（或边所在的直线）相切时，求的值．
如图，四边形OABC是平行四边形，以O为圆心，OA为半径的圆交AB于D，延长 AO交⊙O于E，连接CD，CE，若CE是⊙O的切线，解答下列问题：
（1）求证：CD是⊙O的切线；
（2）若平行四边形OABC的两边长是方程
的两根，求平行四边形OABC的面积．
如图，AB为⊙O的直径，点C在⊙O上，延长BC至点D，使DC=CB，延长DA与⊙O的另一个交点为E，连结AC，CE。
（1）求证：∠B=∠D；
（2）若AB= 
，BC－AC=2，求CE的长。
如图：已知在△ABC中，AB=AC，D为BC边的中点，过点D作DE⊥AB，DF⊥AC，，垂足分别为E，F．
（1）求证：△BED≌△CFD；
（2）若∠A=90°，求证：四边形DFAE是正方形．
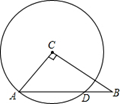
如图，∠C=90°，以AC为半径的⊙C与AB相交于点D．若AC=3，CB=4．求BD长