（本小题满分12分）求经过点P（―3，2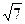
）和Q（―6
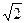，―7）且焦点在坐标轴上的双曲线的标准方程。
（本小题满分12分）已知p：x < －２，或x > 10；q：
≤ｘ≤
；若¬p是q的充分而不必要条件，求实数
的取值范围。
（本小题满分12分）求与双曲线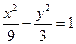
有共同的渐近线，并且经过点
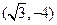的双曲线方程．
(本小题满分16分)
数列
中，
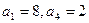且满足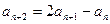
,
，
(1) 求数列的通项公式；
(2) 设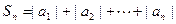
，
求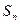
；
(3) 设
，是否存在最大的整数
，使得对任意
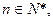均有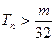
成立？若存在，求出，若
不存在，请说明理由．
(本小题满分16分)
如图,在半径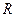为
、圆心角为
的扇形
弧上任取一点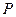
,作扇形的内接矩形
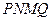,使点
在
上,点
、
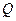在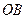
上,求这个矩
形面积的最大值及相应的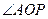
的值.
是定义在
上的奇函数，且
，
的解析式；
.