近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| "厨余垃圾"箱 |
"可回收物"箱 |
"其他垃圾"箱 |
|
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率 ;
(3)假设厨余垃圾在"厨余垃圾"箱、"可回收物"箱、"其他垃圾"箱的投放量分别为
,其中
.当数据
的方差
最大时,写出
的值(结论不要求证明),并求此时
的值.
(注:
,其中
为数据
的平均数)
在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得的成绩,且前5位同学的成绩如下:
编号n: 1, 2, 3, 4, 5
成绩xn:70,76,72,70,72
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选取2位同学,求恰有1位同学的成绩在区间(68,75)中的概率.
有一种密英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不分大小写),依次对应1,2,3,…,26这26个自然数,见如下表格:
| a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
给出如下变换公式:
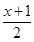 (x∈N,1≤x≤26,x不能被2整除)
(x∈N,1≤x≤26,x不能被2整除)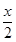 +13(x∈N,1≤x≤26,x能被2整除)
+13(x∈N,1≤x≤26,x能被2整除)
将明文转换成密文,如8→ +13=17,即h变成q;如5→
+13=17,即h变成q;如5→ =3,即e变成c.
=3,即e变成c.
①按上述规定,将明文good译成的密文是什么?
②按上述规定,若将某明文译成的密文是shxc,那么原来的明文是什么?
已知函数f(x)=x3 +x(x∈R).
(1)指出f(x)的奇偶性及单调性,并说明理由;
(2)若a、b、c∈R,且a+b>0,b+c>0,c+a>0,试判断f(a)+f(b)+f(c)的符号.
设命题p:“函数f(x)=ax+1在(-1,1)上存在一个零点”,命题q:“函数f(x)=x2-2ax在(1,+∞)上单调递增”.若“p∨q”为真,“p∧q”为假,求实数a的取值范围.
已知函数 , 若
, 若 2)=1,求
2)=1,求
(1) 实数 的值;
的值;
(2)函数 的值;
的值;
(3)不等式 的解集.
的解集.