设命题p:“函数f(x)=ax+1在(-1,1)上存在一个零点”,命题q:“函数f(x)=x2-2ax在(1,+∞)上单调递增”.若“p∨q”为真,“p∧q”为假,求实数a的取值范围.
(本小题满分11分)已知,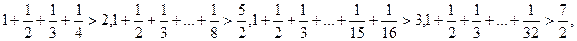
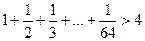 ;
;
(1)试由此归纳出当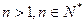 时相应的不等式;
时相应的不等式;
(2)试用数学归纳法证明你在第(1)小题得到的不等式.
(本小题满分11分)已知在 的展开式中,第6项为常数项.
的展开式中,第6项为常数项.
(1)求n;(2)求含x2的项的系数;(3)求展开式中所有的有理项.
(附加题)本题满分20分
如图,已知抛物线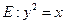
 与圆
与圆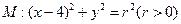 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。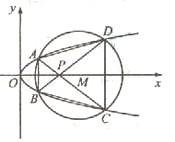
(Ⅰ)求r的取值范围(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;(Ⅱ)求甲获得这次比赛胜利的概率。

(Ⅰ)求 | z1| 的值以及z1的实部的取值范围;(Ⅱ)若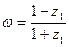 ,求证:
,求证: 为纯虚数
为纯虚数