在直角坐标
中,圆
,圆
.
(Ⅰ)在以
为极点,
轴正半轴为极轴的极坐标系中,分别写出圆
的极坐标方程,并求出圆
的交点坐标(用极坐标表示);
(Ⅱ)求圆
的公共弦的参数方程.
已知函数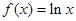 ,
,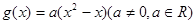 ,
,
(Ⅰ)若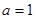 ,求函数
,求函数 的极值;
的极值;
(Ⅱ)若函数 在
在 上单调递减,求实数
上单调递减,求实数 的取值范围;
的取值范围;
(Ⅲ)在函数 的图象上是否存在不同的两点
的图象上是否存在不同的两点 ,使线段
,使线段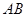 的中点的横坐标
的中点的横坐标 与直线
与直线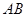 的斜率
的斜率 之间满足
之间满足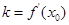 ?若存在,求出
?若存在,求出 ;若不存在,请说明理由.
;若不存在,请说明理由.
已知抛物线 与双曲线
与双曲线 有公共焦点
有公共焦点 ,点
,点 是曲线
是曲线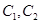 在第一象限的交点,且
在第一象限的交点,且 .
.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)以双曲线 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线 相切,圆
相切,圆 :
: .过点
.过点 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆 相交的直线
相交的直线 和
和 ,设
,设 被圆
被圆 截得的弦长为
截得的弦长为 ,
, 被圆
被圆 截得的弦长为
截得的弦长为 ,问:
,问: 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
知等差数列 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)记 ,求证:
,求证: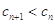 ;
;
(Ⅲ)求数列 的前
的前 项和
项和 .
.
已知四棱锥E-ABCD的底面为菱形,且∠ABC=60°,AB=EC=2,AE=BE= ,O为AB的中点.
,O为AB的中点.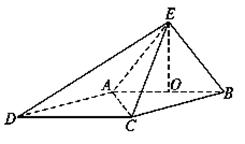
(Ⅰ)求证:EO⊥平面ABCD;
(Ⅱ)求点D到平面AEC的距离.
已知函数 ,若
,若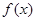 的最大值为1
的最大值为1
(Ⅰ)求 的值,并求
的值,并求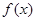 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,角
中,角 、
、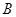 、
、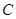 的对边
的对边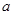 、
、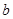 、
、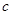 ,若
,若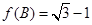 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状.