9月28日,我国神舟七号载人飞船顺利返回地面,下面是“神舟”七号飞船返回舱返回过程中的相关记录:从返回舱制动点火至减速伞打开期间,返回舱距离地面的高度与时间呈二次函数关系,减速伞打开后,返回舱距离地面的高度与时间呈一次函数关系,高度和时间的对应关系如下表:
| 时 间 |
4:45 |
5:12 |
5:15 |
5:18 |
5:24 |
5:26 |
5:28 |
| 返回舱距离地面的高度 |
350km |
134km |
80km |
20km |
8km |
4km |
0km |
| 降落状态 |
返回舱制动点火 |
返回舱高速进入黑障区 |
引导伞引出减速伞 |
减速伞打开 |
返回舱抛掉放热大底 |
着陆系统正式启动 |
返回舱成功降落地面 |
(1) 设减速伞打开后x分钟,返回舱距离地面的高度为hkm,求h与x的函数关系式。
(2) 在返回舱在距离地面5km时,要求宇航员打开电磁信号灯以便地面人员搜寻,判断宇航员应在何时开启信号灯?
点P在图形M上, 点Q在图形N上,记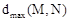 为线段PQ长度的最大值,
为线段PQ长度的最大值,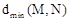 为线段PQ长度的最小值,图形M,N的平均距离
为线段PQ长度的最小值,图形M,N的平均距离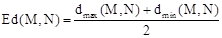 .
.
(1)在平面直角坐标系 中,⊙O是以O为圆心,2的半径的圆,且A
中,⊙O是以O为圆心,2的半径的圆,且A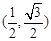 ,B
,B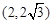 ,求
,求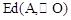 及
及 ;(直接写出答案即可)
;(直接写出答案即可)
(2)半径为1的⊙C的圆心C与坐标原点O重合,直线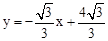 与
与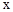 轴交于点D,与
轴交于点D,与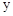 轴交于点F,记线段DF为图形G,求
轴交于点F,记线段DF为图形G,求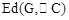 ;
;
(3)在(2)的条件下,如果⊙C的圆心C从原点沿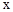 轴向右移动,⊙C的半径不变,且
轴向右移动,⊙C的半径不变,且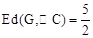 ,求圆心C的横坐标.
,求圆心C的横坐标.
在△ABC中,AB=AC,∠BAC<60°,把线段BC绕点B逆时针旋转60°至BP;如图所示位置有∠ABQ=60°,∠BCQ=150°.
(1)若∠BAC=30°,则∠ABP=度;若∠BAC=α,则∠ABP=(用α表示);
(2)求证:△ABQ为等边三角形;
(3)四边形CBPQ的面积为1,求△ABC的面积.
已知关于 的一元二次方程
的一元二次方程 .
.
(1)若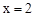 是该方程的一个根,求
是该方程的一个根,求 的值;
的值;
(2)无论 取任何值,该方程的根不可能为
取任何值,该方程的根不可能为 ,写出
,写出 的值,并证明;
的值,并证明;
(3)若 为正整数,且该方程存在正整数解,求所有正整数
为正整数,且该方程存在正整数解,求所有正整数 的值.
的值.
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.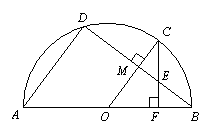
(1)求⊙O的半径;
(2)求证:CE=BE.
已知:如图,在△ABC中,AB="AC=" 5,BC= 8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.