点P在图形M上, 点Q在图形N上,记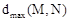 为线段PQ长度的最大值,
为线段PQ长度的最大值,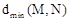 为线段PQ长度的最小值,图形M,N的平均距离
为线段PQ长度的最小值,图形M,N的平均距离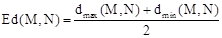 .
.
(1)在平面直角坐标系 中,⊙O是以O为圆心,2的半径的圆,且A
中,⊙O是以O为圆心,2的半径的圆,且A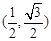 ,B
,B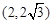 ,求
,求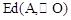 及
及 ;(直接写出答案即可)
;(直接写出答案即可)
(2)半径为1的⊙C的圆心C与坐标原点O重合,直线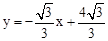 与
与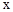 轴交于点D,与
轴交于点D,与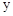 轴交于点F,记线段DF为图形G,求
轴交于点F,记线段DF为图形G,求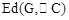 ;
;
(3)在(2)的条件下,如果⊙C的圆心C从原点沿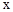 轴向右移动,⊙C的半径不变,且
轴向右移动,⊙C的半径不变,且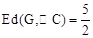 ,求圆心C的横坐标.
,求圆心C的横坐标.
已知 ,求
,求 的值.
的值.
已知:如图,点C,D在线段AB上,E,F在AB同侧,DE与CF相交于点O,且AC=BD,AE=BF,∠A=∠B.求证:DE=CF.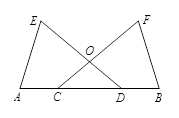
解不等式组 ,并求它的整数解.
,并求它的整数解.
如图,已知直线AC∥BD,直线AB,CD不平行,点P在直线AB上,且和点A、B不重合.
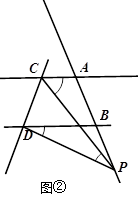
(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)当点P在A、B两点之间运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)(3)如图②,当点P在线段AB延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?并说明理由.
(4)当点P在线段BA延长线上运动时,∠PCA,∠PDB,∠CPD 之间满足什么样的等量关系?(直接写出答案)
“重百”、“沃尔玛”两家超市出售同样的保温壶和水杯,保温壶和水杯在两家超市的售价分别一样.已知买1个保温壶和1个水杯要花费60元,买2个保温壶和3个水杯要花费130元.
(1)请问:一个保温壶与一个水杯售价各是多少元?(列方程组求解)
(2)为了迎接“五一劳动节”,两家超市都在搞促销活动,“重百”超市规定:这两种商品都打九折;“沃尔玛”超市规定:买一个保温壶赠送一个水杯.若某单位想要买4个保温壶和15个水杯,如果只能在一家超市购买,请问选择哪家超市购买更合算?请说明理由.