已知数列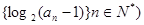 为等差数列,且
为等差数列,且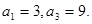
(Ⅰ)求数列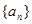 的通项公式;
的通项公式;
(Ⅱ)证明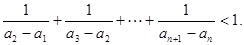
设p :函数y=cx是R上的单调减函数;q:1-2c<0。若p或q是真命题,p 且q是假命题,求c的取值范围。
且q是假命题,求c的取值范围。
设函数 的定义域为集合M,函数
的定义域为集合M,函数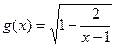 的定义域为集合N.
的定义域为集合N.
求:(1)集合M,N;(2)集合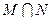 ,
, .
.
已知函数 .
.
(1)用分段函数的形式表示该函数;
(2)画出该函数的图象;
(3)写出该函数的定义域、值域、奇偶性、单调区间.
已知集合A={-1,a2+1,a2-3},B={-4,a-1,a+1},且A∩B={-2},求a的值。
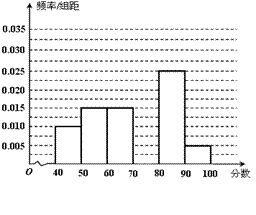
某校从参加高一年级期中考试的学生中随机抽取 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
,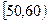 …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在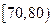 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的平均分;
(Ⅲ)用分层抽样的方法在分数段为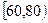 的学生中抽取一个容量为
的学生中抽取一个容量为 的样本,将该样本看成一个总体,从中任取
的样本,将该样本看成一个总体,从中任取 人,求至多有
人,求至多有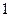 人在分数段
人在分数段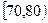 的概率.
的概率.