已知椭圆C: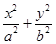 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为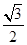 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为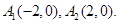
(1)求椭圆方程;
(2)若直线 :
: 与
与 轴交于点T,P为
轴交于点T,P为 上异于T的任一点,直线
上异于T的任一点,直线 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
(本小题满分12分)
已知点 ,点
,点 在
在 轴上,点
轴上,点 在
在 轴的正半轴上,点
轴的正半轴上,点 在直线
在直线 上,且
上,且
满足 .
.
(Ⅰ)当点 在
在 轴上移动时,求点
轴上移动时,求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设 、
、 为轨迹
为轨迹 上两点,且
上两点,且 >1,
>1,  >0,
>0, ,求实数
,求实数 ,
,
使 ,且
,且 .
.
(本小题满分12分) 已知 为坐标原点,点
为坐标原点,点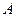 、
、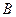 分别在
分别在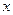 轴、
轴、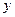 轴上运动,且
轴上运动,且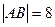 ,动点
,动点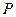 满足
满足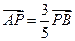 ,设点
,设点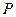 的轨迹为曲线
的轨迹为曲线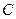 ,定点
,定点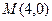 ,直线
,直线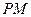 交曲线
交曲线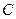 于另外一点
于另外一点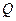 .
.
(1)求曲线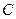 的方程;
的方程;
(2)求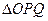 面积的最大值.
面积的最大值.
(本小题满分13分)如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线L在y轴上的截距为m(m≠0),L交椭圆于A、B两个不同点。
(1)求椭圆的方程;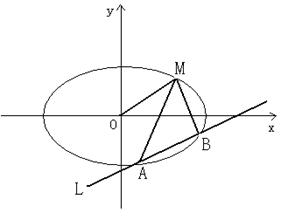
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形。
已知数列( )与{
)与{ )有如下关系:
)有如下关系: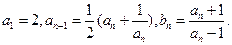
(1)求数列( }的通项公式。
}的通项公式。
(2)设 是数列{
是数列{ }的前n项和,当n≥2时,求证
}的前n项和,当n≥2时,求证 :
:
(本小题满分13分)已知函数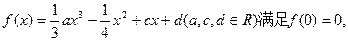
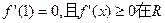 上恒成立.
上恒成立.
(1)求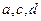 的值;
的值;
(2)若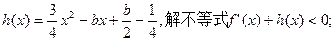
(3)是否存在实数m,使函数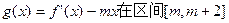 上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.
上有最小值-5?若存在,请求出实数m的值;若不存在,请说明理由.