如图,AB是⊙O的直径,点C在AB延长线上,点D在⊙O上,连接AD,BD,BO=BC=BD,OE⊥BD于E,连接AE.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为4,求AE的长.
某职业学校三名学生到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话。
A:如果以10元/千克的价格销售,那么每天可售出300千克.
B:如果以13元/千克的价格销售,那么每天可获取利润750元.
C:通过调查验证,我发现每天的销售量y(千克)与销售单价x(元)之间存在一次函数关系.
(1)求y(千克)与x(元)(x>0)的函数关系式;
(2)当销售单价为何值时,该超市销售这种水果每天获取的利润达到600元?【利润=销售量×(销售单价-进价)】
(3)一段时间后,发现这种水果每天的销售量均不低于225千克.则此时该超市销售这种水果每天获取的最大利润是多少?
如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.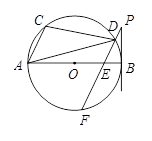
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=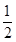 ,求AC的长.
,求AC的长.
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=60°,∠BEQ=45°;在点F处测得∠AFP=45°,∠BFQ=90°,EF=2km.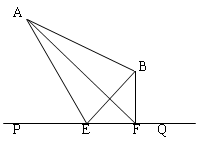
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果保留根号).
已知:平行四边形ABCD中,E、F是BC、AB的中点,DE、DF分别交AB、CB的延长线于H、G;
(1)求证:BH =AB;
(2)若四边形ABCD为菱形,试判断∠G与∠H的大小关系,并证明你的结论.
有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式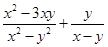 有意义的(x,y)出现的概率
有意义的(x,y)出现的概率