已知函数 在
在 处取得极值,
处取得极值,
(1)求实数 的值;
的值;
(2)若关于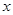 的方程
的方程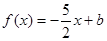 在区间
在区间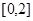 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数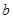 的取值范围.
的取值范围.
如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
已知两条直线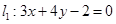 与
与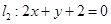 的交点
的交点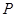 ,求:(1)过点
,求:(1)过点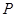 且过原点的直线方程;(2)过点
且过原点的直线方程;(2)过点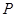 且垂直于直线
且垂直于直线 的直线
的直线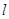 的方程。
的方程。
直三棱柱
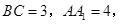
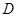 是
是 的中点.
的中点.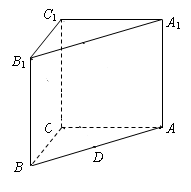
(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
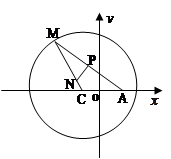
如图所示,已知圆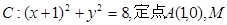 为圆上一动点,点
为圆上一动点,点 在
在 上,点
上,点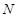 在
在 上,且满足
上,且满足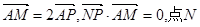 的轨迹为曲线
的轨迹为曲线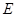 .
.
(1)求曲线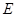 的方程;
的方程;
(2)若直线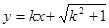 与(1)中所求点
与(1)中所求点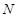 的轨迹
的轨迹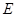 交于不同两点
交于不同两点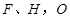 是坐标原点,且
是坐标原点,且 ,求△
,求△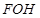 的面积的取值范围.
的面积的取值范围.
【改编】如图,在边长为1的等边三角形 中,
中, 分别是
分别是 边上的点,
边上的点, ,
, 是
是 的中点,
的中点, 与
与 交于点
交于点 ,将
,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,得到如图所示的三棱锥
,得到如图所示的三棱锥 .
.
(1)证明: //平面
//平面 ;
;
(2)证明:
 平面
平面 ;
;
(3)当 时,求三棱锥
时,求三棱锥 的体积
的体积 .
.