如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
已知函数f(x)=ax2+bx+1(a,b为常数),x∈R.F(x)= .
.
(1)若f(-1)=0,且函数f(x)的值域为[0,+∞),求F(x)的表达式;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围;
(3)设m·n<0,m+n>0,a>0,且f(x)为偶函数,判断F(m)+F(n)能否大于零?
已知f(x)=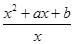 ,x∈(0,+∞).
,x∈(0,+∞).
(1)若b≥1,求证:函数f(x)在(0,1)上是减函数;
(2)是否存在实数a,b,使f(x)同时满足下列两个条件:
①在(0,1)上是减函数,(1,+∞)上是增函数;
②f(x)的最小值是3.若存在,求出a,b的值;若不存在,请说明理由.
已知 是定义在
是定义在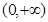 上的增函数,且满足
上的增函数,且满足 ,
,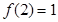 。
。
(1)求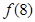
(2)求不等式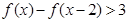 的解集
的解集
已知函数 满足
满足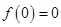 ,且
,且 ,令
,令 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数 的最小值.
的最小值.
已知集合A={x|2a+1≤x≤3a-5},B={x|x<-1,或x>16},分别根据下列条件求实数a的取值范围.
(1)A∩B= ;(2)A⊆(A∩B).
;(2)A⊆(A∩B).