图1中所示的遮阳伞,伞柄垂直于地面,其示意图如图2.当伞收紧时,点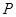 与点
与点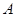 重合(此时AC=PN+CN);当伞慢慢撑开时,动点
重合(此时AC=PN+CN);当伞慢慢撑开时,动点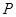 由
由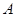 向
向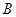 移动;当点
移动;当点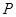 到过点
到过点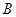 时,伞张得最开.已知伞在撑开的过程中,总有
时,伞张得最开.已知伞在撑开的过程中,总有 分米,
分米,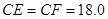 分米,
分米, 分米
分米
(1)求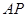 长的取值范围; (2)当
长的取值范围; (2)当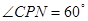 时,求
时,求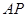 的值;
的值;
(3)在阳光垂直照射下,伞张得最开,求伞下的阴影(假定为圆面)面积为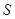 (结果保留
(结果保留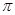 ).
).
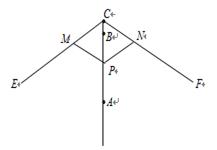
如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC= ,求AB.
,求AB.
如图,已知一次函数 与反比例函数
与反比例函数 的图象交于A,B两点.求A,B两点的坐标.
的图象交于A,B两点.求A,B两点的坐标.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,即OD⊥AB于点D,OE⊥AC于点E,OD=OE,且OB=OC。

(1)如图,若点O在BC上,求证:AB=AC;
(2)如图,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示(只需画图即可)。
在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙基C处7米.
(1)求这个梯子的顶端距地面有多高?
(2)如果消防员接到命令,要求梯子的顶端A下降4米至E处(云梯长度不变),那么云梯的底部在水平方向滑动距离BF为多少米?
如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC,垂足为M。求证:M是BE的中点。