(本小题满分12分)直线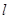 与椭圆
与椭圆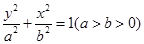 交于
交于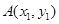 ,
, 两点,已知
两点,已知
 ,
,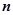
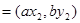 ,若
,若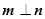 且椭圆的离心率
且椭圆的离心率 ,又椭圆经过点
,又椭圆经过点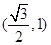 ,
, 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线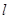 过椭圆的焦点
过椭圆的焦点 (
(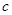 为半焦距),求直线
为半焦距),求直线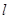 的斜率
的斜率 的值;
的值;
(Ⅲ)试问: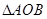 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
(本小题满分16分)记公差d≠0的等差数列{an}的前n项和为Sn,已知a1=2+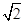 ,S3=12+
,S3=12+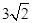 .
.
(1)求数列{an}的通项公式an及前n项和Sn;
(2)记bn=an-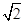 ,若自然数n1,n2,…,nk,…满足1≤n1<n2<…<nk<…,并且
,若自然数n1,n2,…,nk,…满足1≤n1<n2<…<nk<…,并且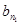 ,
,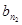 ,…,
,…,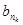 ,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
(3)试问:在数列{an}中是否存在三项ar,as,at(r<s<t,r,s,t∈N*)恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
(本小题满分15分)已知椭圆C: +
+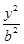 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为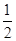 ,且经过点P(1,
,且经过点P(1,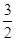 ).
).
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M.问点M满足什么条件时,圆M与y轴有两个交点? 并求两点间距离的最大值.
(本小题满分15分)
因发生意外交通事故,一辆货车上的某种液体泄漏到一渔塘中.为了治污,根据环保部门的建议,现决定在渔塘中投放一种可与污染液体发生化学反应的药剂.已知每投放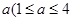 ,且
,且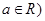 个单位的药剂,它在水中释放的浓度
个单位的药剂,它在水中释放的浓度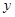 (克/升)随着时间
(克/升)随着时间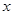 (天)变化的函数关系式近似为
(天)变化的函数关系式近似为 ,其中
,其中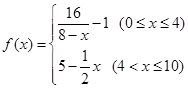 .
.
若多次投放,则某一时刻水中的药剂浓度为每次投放的药剂在相应时刻所释放的浓度之和.根据经验,当水中药剂的浓度不低于4(克/升)时,它才能起到有效治污的作用.
(1)若一次投放4个单位的药剂,则有效治污时间可达几天?
(2)若第一次投放2个单位的药剂,6天后再投放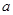 个单位的药剂,要使接下来的4天中能够持续有效治污,试求
个单位的药剂,要使接下来的4天中能够持续有效治污,试求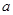 的最小值.(精确到0.1,参考数据:
的最小值.(精确到0.1,参考数据: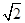 取1.4)
取1.4)
(本小题满分14分)如图,在直三棱柱ABC—A1B1C1中,AB=AC,点D是BC的中点.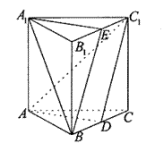
(1)求证:A1B//平面ADC1;
(2)如果点E是B1C1的中点,求证:平面 平面BCC1B1.
平面BCC1B1.
(本小题满分14分)已知△ABC的三个内角A、B、C所对的边分别为a、b、c,向量m=(sinA,1),n=(1,- cosA),且m⊥n.
cosA),且m⊥n.
(1)求角A;
(2)若b+c= a,求sin(B+
a,求sin(B+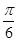 )的值.
)的值.