如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒).
(1)当t=2时,求△BPQ的面积;
(2)若四边形ABQP为平行四边形,求运动时间t.
(3)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线 ,点 、 分别在 、 上,斜坡 的长为18米,过点 作 于点 ,且线段 的长为 米.
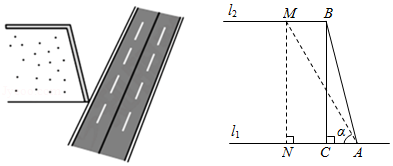
(1)求该斜坡的坡高 ;(结果用最简根式表示)
(2)为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡角 为 ,过点 作 于点 ,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?
先化简,再求值: ,其中 , .
计算: .
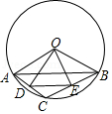
如图,半径为4的 中,弦 的长度为 ,点 是劣弧 上的一个动点,点 是弦 的中点,点 是弦 的中点,连接 、 、 .
(1)求 的度数;
(2)当点 沿着劣弧 从点 开始,逆时针运动到点 时,求 的外心 所经过的路径的长度;
(3)分别记 , 的面积为 , ,当 时,求弦 的长度.
我们不妨约定:若某函数图象上至少存在不同的两点关于原点对称,则把该函数称之为“ 函数”,其图象上关于原点对称的两点叫做一对“ 点”.根据该约定,完成下列各题.
(1)在下列关于 的函数中,是“ 函数”的,请在相应题目后面的括号中打“ ”,不是“ 函数”的打“ ”.
① ;
② ;
③ .
(2)若点 与点 是关于 的“ 函数” 的一对“ 点”,且该函数的对称轴始终位于直线 的右侧,求 , , 的值或取值范围.
(3)若关于 的“ 函数” , , 是常数)同时满足下列两个条件:① ,② ,求该“ 函数”截 轴得到的线段长度的取值范围.