.已知 是复数,
是复数, ,
, 均为实数(
均为实数( 为虚数单位)且复数
为虚数单位)且复数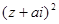 在复平面上对应的点在第一象限,求复数
在复平面上对应的点在第一象限,求复数 及实数
及实数 的取值范围.
的取值范围.
(本小题满分12分)已知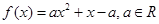 .
.
(Ⅰ)若不等式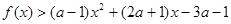 对任意实数
对任意实数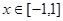 恒成立,求实数
恒成立,求实数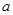 的取值范围;
的取值范围;
(Ⅱ)若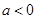 ,解不等式
,解不等式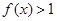 .
.
(本小题满分12分)设数列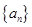 的各项均为正数,它的前
的各项均为正数,它的前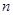 项的和为
项的和为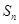 ,且
,且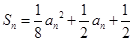 ,数列
,数列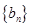 满足
满足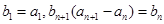 .其中
.其中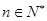 .
.
(Ⅰ)求数列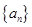 和
和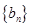 的通项公式;
的通项公式;
(Ⅱ)设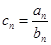 ,求证:数列
,求证:数列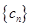 的前
的前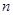 项的和
项的和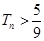 (
(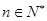 ).
).
(本小题满分12分)已知函数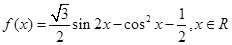 .
.
(Ⅰ)求函数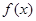 的最小值,及取最小值时
的最小值,及取最小值时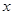 的值;
的值;
(Ⅱ)设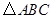 的内角
的内角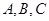 的对边分别为
的对边分别为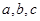 且
且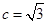 ,
,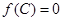 ,若
,若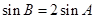 ,求
,求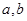 的值.
的值.
(本小题满分12分)已知等差数列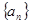 的公差
的公差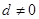 ,该数列的前
,该数列的前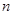 项和为
项和为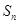 ,且满足
,且满足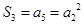 .
.
(Ⅰ)求数列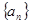 的通项公式;
的通项公式;
(Ⅱ)设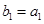 ,
,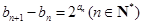 ,求数列
,求数列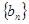 的通项公式.
的通项公式.
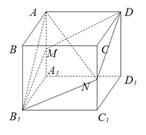
(本小题满分12分)已知正方体 的棱长为
的棱长为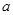 ,
,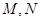 分别是棱
分别是棱 的中点,
的中点,
(Ⅰ)求正方体 的内切球的半径与外接球的半径之比;
的内切球的半径与外接球的半径之比;
(Ⅱ)求四棱锥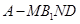 的体积.
的体积.