(本小题满分12分)
已知椭圆 的离心率
的离心率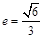 ,过点
,过点 和
和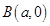 的直线与原点的距离为
的直线与原点的距离为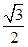 。⑴求椭圆的方程;⑵已知定点
。⑴求椭圆的方程;⑵已知定点 ,若直线
,若直线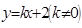 与椭圆交于
与椭圆交于 两点,问:是否存在
两点,问:是否存在 的值,使以
的值,使以 为直径的圆过
为直径的圆过 点?请说明理由。
点?请说明理由。
(本小题满分12分)一个四棱锥的直观图和三视图如图所示: 

(1)求证: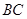 ⊥
⊥ ;
;
(2)求出这个几何体的体积。
(3)若在PC上有一点E,满足CE:EP=2:1,求证PA//平面BED。
已知直线 与圆
与圆 的交点为A、B,
的交点为A、B,
(1)求弦长AB;
(2)求过A、B两点且面积最小的圆的方程.
(本小题满分12分)
设函数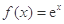 (
(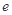 为自然对数的底数),
为自然对数的底数), (
(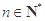 ).
).
(1)证明: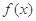
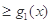 ;
;
(2)当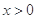 时,比较
时,比较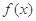 与
与 的大小,并说明理由;
的大小,并说明理由;
(3)证明: (
(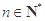 ).
).
(本小题满分12分)
已知数列 的相邻两项
的相邻两项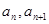 是关于
是关于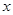 的方程
的方程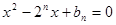
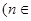 N
N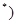 的两根,且
的两根,且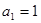 .
.
(1) 求数列 和
和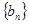 的通项公式;
的通项公式;
(2) 设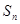 是数列
是数列 的前
的前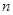 项和, 问是否存在常数
项和, 问是否存在常数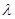 ,使得
,使得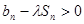 对任意
对任意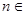 N
N 都成立,若存在, 求出
都成立,若存在, 求出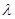 的取值范围; 若不存在, 请说明理由.
的取值范围; 若不存在, 请说明理由.