实践应用(本小题满分8分)
已知A、B两地相距300千米,甲、乙两车同时从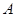 地出发,以各自的速度匀速往返两地.甲车先到达
地出发,以各自的速度匀速往返两地.甲车先到达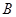 地,停留1小时后按原路返回.设两车行驶的时间为
地,停留1小时后按原路返回.设两车行驶的时间为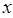 小时,离开
小时,离开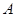 地的距离是
地的距离是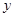 千米,如图是
千米,如图是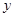 与
与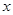 的函数图象.
的函数图象.
(1)计算甲车的速度为 ▲ 千米/时,乙车的速度为 ▲ 千米/时;
(2) 几小时后两车相遇;
(3) 在从开始出发到两车相遇的过程中,设两车之间的距离为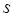 千米,乙车行驶的时间为
千米,乙车行驶的时间为 小时,求
小时,求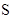 与
与 之间的函数关系式.
之间的函数关系式.
某中学计划从办公用品公司购买A,B两种型号的小黑板.经洽谈,购买一块A型小黑板比购买一块B型小黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820元.
(1)求购买一块A型小黑板、一块B型小黑板各需多少元.
(2)根据该中学实际情况,需从公司购买A,B两种型号的小黑板共60块,要求购买A,B两种型号小黑板的总费用不超过5240元.并且购买A型小黑板的数量不小于购买B型小黑板数量的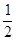 .则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
.则该中学从公司购买A,B两种型号的小黑板有哪几种方案?哪种方案的总费用最低?
如图,已知一次函数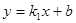 与反比例函数
与反比例函数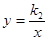 的图象交于两点A(-1,6),B(a,3).
的图象交于两点A(-1,6),B(a,3).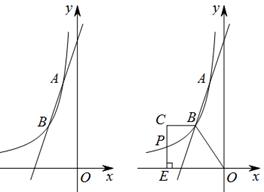
(1)求两个函数的解析式;
(2)结合图形,直接写出时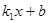 -
-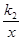 ﹥0时
﹥0时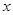 的取值范围;
的取值范围;
(3)如图2,梯形OBCE中,BC∥OE,过点C作CE⊥x轴于点E,CE和反比例函数的图象交于点P,当梯形OBCE的面积为9时,请求出点P的坐标.
如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,在□ABCD中,延长CD到E,使DE=CD,连接BE,交AD于点F,交AC于点G.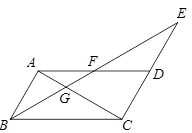
(1)求证:AF=DF;
(2)若BC=2AB,且DE=1,∠E=30°,求BE的长.
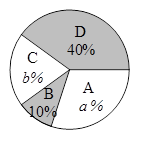
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图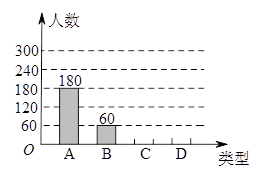
请根据以上信息回答:
(1)本次参加抽样调查的居民有________人;
(2)扇形统计图中:a=________,b=_________,并把条形统计图补充完整;
(3)若有外型完全相同的A,B,C,D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.