牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
销售单价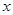 (元/件) (元/件) |
… |
20 |
30 |
40 |
50 |
60 |
… |
每天销售量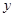 (件) (件) |
… |
500 |
400 |
300 |
200 |
100 |
… |
(1)把上表中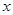 、
、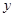 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想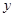 与
与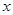 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价﹣成本总价)
(3)菏泽市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?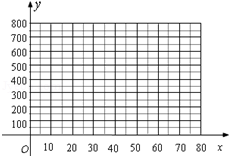
(年安徽省12分)若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”.
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数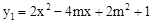 ,和
,和 ,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值.
,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值.
(年福建厦门10分)如图,已知c<0,抛物线y=x2+bx+c与x轴交于A(x1,0),B(x2,0)两点(x2>x1),与y轴交于点C.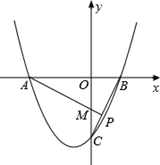
(1)若x2=1,BC= ,求函数y=x2+bx+c的最小值;
,求函数y=x2+bx+c的最小值;
(2)过点A作AP⊥BC,垂足为P(点P在线段BC上),AP交y轴于点M.若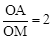 ,求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.
,求抛物线y=x2+bx+c顶点的纵坐标随横坐标变化的函数解析式,并直接写出自变量的取值范围.
(年四川巴中10分)如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数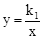 (x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为
(x>0)的图象经过线段OC的中点A,交DC于点E,交BC于点F.设直线EF的解析式为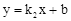 .
.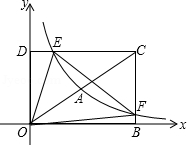
(1)求反比例函数和直线EF的解析式;
(2)求△OEF的面积;
(3)请结合图象直接写出不等式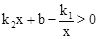 的解集.
的解集.
(年山东枣庄10分)如图,一次函数y=ax+b与反比例函数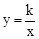 的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为
的图象交于A、B两点,点A坐标为(m,2),点B坐标为(﹣4,n),OA与x轴正半轴夹角的正切值为 ,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.
,直线AB交y轴于点C,过C作y轴的垂线,交反比例函数图象于点D,连接OD、BD.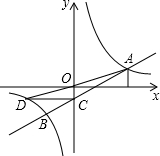
(1)求一次函数与反比例函数的解析式;
(2)求四边形OCBD的面积.
(2014年江苏淮安12分)如图,点A(1,6)和点M(m,n)都在反比例函数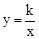 (x>0)的图象上。
(x>0)的图象上。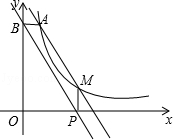
(1)k的值为 ;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.