某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50
元销售,一个月能售出500㎏,销售单价每涨1元,月销售量就减少10㎏,针对这种水产
品,请解答以下问题:
⑴当销售单价定为每千克55元时,计算销售量与月销售利润;
⑵设销售单价为每千克 元,月销售利润为
元,月销售利润为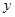 元,求
元,求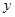 与
与 的关系式;
的关系式;
⑶当销售单价为多少时,月销售利润最大?最大利润是多少?
⑷商店想在销售成本不超过10000元的情况下,使得月销售利润刚好达到8000元,销售单价应为多少?
右表反映了x与y之间存在某种函数关系,现给出了几种可能的函数关系式:
y=x+7,y=x-5, ,
,
| x |
… |
-6 |
-5 |
3 |
4 |
… |
| y |
… |
1 |
1.2 |
-2 |
-1.5 |
… |
(1)从所给出的几个式子中选出一个你认为满足上表要求的函数表达式:;
(2)请说明你选择这个函数表达式的理由.
列方程解应用题:
今年“六•一”儿童节,张红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件?
计算:
如图所示,二次函数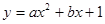 (
(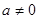 )的图像与
)的图像与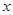 轴分别交于
轴分别交于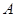 (
(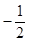 ,
, )、
)、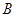 (
(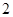 ,
, )两点,且与
)两点,且与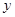 轴交于点
轴交于点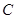 ;
;
(1)求该拋物线的解析式,并判断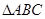 的形状;
的形状;
(2)在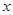 轴上方的拋物线上有一点
轴上方的拋物线上有一点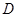 ,且以
,且以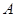 、
、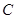 、
、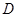 、
、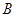 四点为顶点的四边形是等腰梯形,请直接写
四点为顶点的四边形是等腰梯形,请直接写
出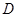 点的坐标;
点的坐标;
(3)在此拋物线上是否存在点P,使得以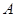 、
、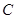 、
、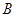 、
、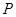 四点为顶点的四边形是直角梯形?若存在,求
四点为顶点的四边形是直角梯形?若存在,求
(4)出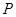 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.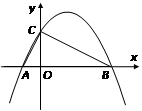
如图,在平面直角坐标系中,一次函数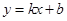 的图象分别交x轴、y轴于A、B两点,与反比例函数
的图象分别交x轴、y轴于A、B两点,与反比例函数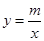 的图象交于C、D两点,DE⊥x轴于点E。已知C点的坐标是(6,
的图象交于C、D两点,DE⊥x轴于点E。已知C点的坐标是(6,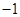 ),DE=3.
),DE=3.
(1)求反比例函数与一次函数的解析式。
(2)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?