列方程解应用题:
今年“六•一”儿童节,张红用8.8元钱购买了甲、乙两种礼物,甲礼物每件1.2元,乙礼物每件0.8元,其中甲礼物比乙礼物少1件,问甲、乙两种礼物各买了多少件?
2012年秋冬北方干旱,光明社区出现饮用水紧张,每天需从社区外调运饮用水120吨.现从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨.从两水厂运水到光明社区供水点的路程和运费如下表:
| 到光明社区供水点的路程(千米) |
运费(元/吨 千米) 千米) |
|
| 甲厂 |
20 |
12 |
| 乙厂 |
14 |
15 |
(1)若某天调运水的总运费为26700元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设某天从甲厂调运饮用水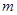 吨,总运费为
吨,总运费为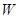 元,试写出
元,试写出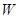 关于
关于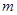 的函数关系式,并求出这天运费最少为多少元?
的函数关系式,并求出这天运费最少为多少元?
先化简,再求值: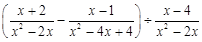 ,其中
,其中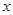 是不等式组
是不等式组 的整数解.
的整数解.
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(0,1),B(–1,1),C(–1,3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2;
(3)C1的坐标为,C2的坐标为,在(2)中点A旋转到A2经过的路径长为.
计算: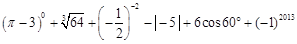 .
.
操作:在△ABC中,AC=BC=2,∠C=90°,将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点(不包括射线的端点).如图1,2,3是旋转三角板得到的图形中的3种情况.
研究: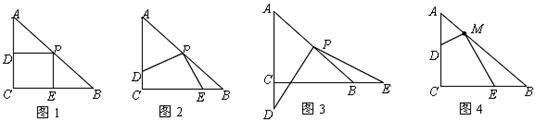
⑴三角板绕点P旋转,观察线段PD和PE之间有什么数量关系?并结合如图2加以证明.
⑵三角板绕点P旋转,△PBE是否能成为等腰三角形?若能,指出所有情况(即写出△PBE为等腰三角形时CE的长;若不能,请说明理由.
⑶若将三角板的直角顶点放在斜边AB上的M处,且AM∶MB=1∶3,和前面一样操作,试问线段MD和ME之间有什么数量关系?并结合如图4加以证明.