已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的单调区间.
的单调区间.
((本小题满分12分) 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],……,(510,515],由此得到样本的频率分布直方图,如图4所示.
(Ⅰ)根据频率分布直方图,求重量超过500 克的产品数量;
(Ⅱ)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量, 求Y的分布列及数学期望.
(本小题满分12分) 已知向量 =(
=(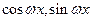 ),
),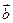 =(
=( ,
,
 ),其中(
),其中( ).函数,
).函数,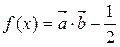 其图象的一条对称轴为
其图象的一条对称轴为 .
.
(I)求函数 的表达式及单调递增区间;
的表达式及单调递增区间;
(Ⅱ)在△ABC中,a、b、c分别为角A、B、C的对边,S为其面积,若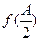 =1,b=l,
=1,b=l,
S△ABC=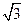 ,求a的值.
,求a的值.
(本小题满分12分)
已知数列 满足:
满足: ,其中
,其中 为数列
为数列 的前
的前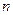 项和.
项和.
(Ⅰ)试求 的通项公式;
的通项公式;
(Ⅱ)若数列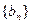 满足:
满足: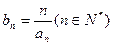 ,试求
,试求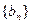 的前
的前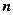 项和公式
项和公式 .
.
设函数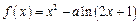 (
( ,
, ).
).
(1)若函数 在其定义域内是减函数,求
在其定义域内是减函数,求 的取值范围;
的取值范围;
(2)函数 是否有最小值?若有
是否有最小值?若有 最小值,指出其取得最小值时
最小值,指出其取得最小值时 的值,并证明你的结论.
的值,并证明你的结论.
已知椭圆C的中心在原点,焦点在 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为 .
.
(1)求椭圆C的标准方程;
(2)若直线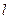 :
: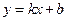 与圆O:
与圆O: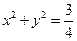 相切,且交椭圆C于A、B两点,
相切,且交椭圆C于A、B两点,
求当△AOB的面积最大时直线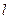 的方程.
的方程.