若点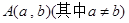 在矩阵
在矩阵

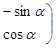 对应变换的作用下得到的点为
对应变换的作用下得到的点为
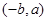 ,(Ⅰ)求矩阵
,(Ⅰ)求矩阵 的逆矩阵;
的逆矩阵;
(Ⅱ)求曲线C:x2+y2=1在矩阵N= 所对应变换的作用下得到的新的曲线C'的方程.
所对应变换的作用下得到的新的曲线C'的方程.
甲盒中有1个黑球1个白球;乙盒中有1个黑球2个红球.这些 球除了颜色不同外其余无差别.
球除了颜色不同外其余无差别.
(Ⅰ)从两个盒子中各取1个球,求取出的两个球颜色不同的概率.
(Ⅱ)若把两盒中所有的球混合后放入丙盒中.从丙盒中一次取出两个球,求取出的两个球颜色不同的概率 .
.
(本题12分)
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD= ,底面ABCD为直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC="2," O为AD中点.
,底面ABCD为直角梯形,BC∥AD,AB⊥AD,AD=2AB=2BC="2," O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求直线PB与平面PAD所成角的正弦值;
(3)线段AD上是否存在点Q,使得三棱锥 的体积为
的体积为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本题12分)
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,∠PDA=45°,点E、F分别为棱AB、PD的中点.
(1)求证: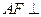 平面PCD;(2)求证:平面PCE⊥平面PCD.
平面PCD;(2)求证:平面PCE⊥平面PCD.
 |
(本题12分)
如图,在直三棱柱(侧棱与底面垂直的三棱柱)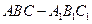 中,
中,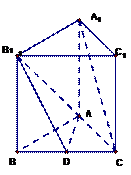
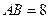 ,
,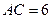 ,
,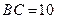 ,
,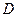 是
是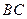 边的中点.
边的中点.
(Ⅰ)求证: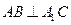 ;
;
(Ⅱ)求证: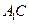 ∥面
∥面 .
.
(本题12分)
已知函数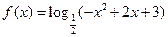
(1)求 的定义域;
的定义域;
(2)求 的值域。
的值域。