直角梯形ABCD中，AD∥BC,AB=AD=3，边BC, AB分别在x轴和y轴上，已知点C的坐标分别为（4,0）。动点P从B点出发，以每秒1个单位的速度沿BC方向作匀速直线运动，同时点Q从D点出发，以与P点相同的速度沿DA方向运动，当Q点运动到A点时, P,Q两点同时停止运动。设点P运动时间为t，
(1)求线段CD的长。
(2) 连接PQ交直线AC于点E，当AE : EC="1" : 2时，求t的值，并求出此时△PEC的面积。
(3) 过Q点作垂直于AD的射线交AC于点M，交BC于点N，连接PM，
①是否存在某一时刻，使以Ｍ、P、Ｃ三点为顶点的三角形是等腰三角形？若存在 ，求出此时t的值；若不存在，请说明理由；
②当t= 时，点P、M、D在同一直线上。（直接写出）
|
如图，在每个小正方形的边长均为1个单位长度的方格纸中，有线段AB和直线MN，点A、B、M、N均在小正方形的顶点上．
（1）在方格纸中画四边形ABCD(四边形的各顶点均在小正方形的顶点上)，使四边形ABCD是以直线MN为对称轴的轴对称图形，点A的对称点为点D，点B的对称点为点C；
（2）若直线MN上存在点P，使得PA＋PB的值最小，请直接写出PA的长度．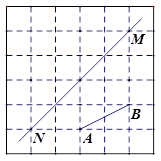
如图，△ABC内接于⊙O，弦AD⊥AB交BC于点E，过点B作⊙O的切线交DA的延长线于点F，且∠ABF＝∠ABC．
（1）求证：AB＝AC；
（2）若AD＝4，cos∠ABF＝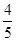
，求DE的长．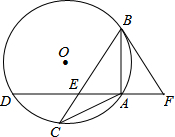
如图，在平行四边形ABCD中，E为BC边上的一点，连接AE、BD交于点F，AE＝AB.
（1）若∠AEB＝2∠ADB，求证：四边形ABCD是菱形.
（2）若AB＝10，BE＝2EC，求EF的长.
某区八年级有3000名学生参加“爱我中华知识竞赛”活动．为了了解本次知识竞赛的成绩分布情况，从中抽取了200名学生的得分进行统计．
请你根据不完整的表格，回答下列问题：
| 成绩x |
频数 |
频率 |
| 50≤x＜60 |
10 |
____ |
| 60≤x＜70 |
16 |
0.08 |
| 70≤x＜80 |
____ |
0.20 |
| 80≤x＜90 |
62 |
____ |
| 90≤x＜100 |
72 |
0.36 |
（1）补全频数分布直方图；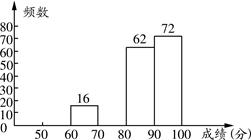
（2）若将得分转化为等级，规定50≤x＜60评为“D”，60≤x＜70评为“C”，70≤x＜90评为“B”，90≤x＜100评为“A”．这次全区八年级参加竞赛的学生约有多少学生参赛成绩被评为“D”？
列方程或方程组解应用题：
某停车场的收费标准如下：中型汽车的停车费为每辆6元，小型汽车的停车费为每辆4元. 现在停车场有中、小型汽车共50辆，这些车共缴纳停车费230元，问中、小型汽车各有多少辆？