如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PE⊥AB交AC于点E．
（1）直接写出点A的坐标，并求出抛物线的解析式；
（2）过点E作EF⊥AD于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？
（3）在动点P，Q运动的过程中，当t为何值时，在矩形ABCD内（包括边界）存在点H，使以C，Q，E，H为顶点的四边形为菱形？请直接写出t的值．
把命题改写成”如果…那么…”的形式．
（1）对顶角相等．
（2）两直线平行，同位角相等．
（3）等角的余角相等．
命题：若a＞b，则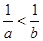
．
（1）请判断这个命题的真假．若是真命题请证明；若是假命题，请举一个反例；
（2）请你适当修改命题的题设使其成为一个真命题．
如图，抛物线y＝mx2―2mx―3m（m＞0）与x轴交于A、B两点， 与y轴交于C点。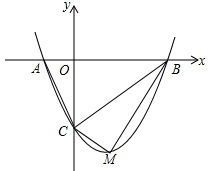
（1）请求抛物线顶点M的坐标（用含m的代数式表示），A，B两点的坐标；
（2）经探究可知，△BCM与△ABC的面积比不变，试求出这个比值；
如图所示，已知正方形ABCD中，BE平分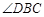
且交CD边于点E。将△BCE绕点C顺时针旋转到△DCF的位置，并延长BE交DF于点G。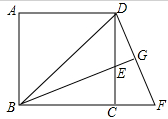
（1）求证：△BDG∽△DEG；
（2）若EG·BG=4，求BE的长。
如图，在Rt△ABC中，∠B=90°，∠BAC的平分线交BC于点D，E为AB上的一点，DE=DC，以D为圆心，DB长为半径作⊙D，AB=5，EB=3。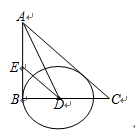
（1）求证：AC是⊙O的切线；
（2）求线段AC的长。