如图,直线y=kx+b与反比例函数 只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
只有一个交点A(1 , 2),且与x轴、y轴分别交于B,C两点,AD垂直平分OB,垂足为D,
(1)求点B的坐标和m的值;
(2)求直线解析式
已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,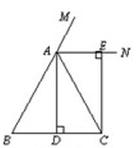
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
请认真阅读题意,并根据你的发现填空:
(1)将任何一组已知的勾股数中的每一个数都扩大为原来的正整数倍后,就得到一组新的勾股数,例如:3、4、5,我们把每一个数扩大为原来的2倍、3倍,则分别得到6、8、10和9、12、15,
若把每一个数都扩大为原来的12倍,就得到______________,
若把每一数都扩大为原来的n(n为正整数)倍,则得到_________________;
(2)对于任意一个大于1的奇数,存在着下列勾股数
若勾股数为3、4、5.则有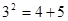
若勾股数为5、12、13, 则有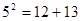
若勾股数为7、24、25, 则有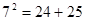
若勾股数为m(m为奇数)、n、______
则有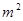 =2n+1,用m表示n=_______
=2n+1,用m表示n=_______
当m=17时,n=_______,此时勾股数为_______________.
△ABC中,AC=8,BC=6,在△ABE中,DE为AB边上的高,DE=12,S△ABE=60,求∠C的度数.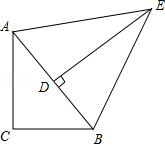
已知:如图,D、E、F是△ABC各边的中点,FG∥CD交ED的延长线于点G,AC=6,求GD的长度
已知:如图,双曲线 的图象经过A(1,2)、B(2,b)两点.
的图象经过A(1,2)、B(2,b)两点.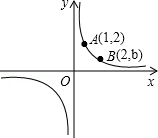
(1)求双曲线的解析式;
(2)当1<x<2时,反比例函数函数值的取值范围.