咖啡馆配制两种饮料，甲种饮料每杯分别用奶粉、咖啡、糖9g、4g、3g；乙种饮料每杯分别用奶粉、咖啡、糖4g、5g、10g，已知每天使用原料限额为奶粉3600g，咖啡2000g，糖3000g，如果甲种饮料每杯能获利0.7元，乙种饮料每杯能获利1.2元，每天在原料使用的限额内，饮料能全部售完，问咖啡馆每天怎样安排配制饮料获利最大？
已知函数f(x)＝lnx－ax2＋(2－a)x.
(1)讨论f(x)的单调性；
(2)设a>0，证明：当0<x<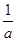
时，f
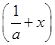>f
；
(3)若函数y＝f(x)的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：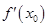
＜0.
已知函数f(x)＝ax＋x2－xlna(a>0，a≠1)．
(1)当a>1时，求证：函数f(x)在(0，＋∞)上单调递增；
(2)若函数y＝|f(x)－t|－1有三个零点，求t的值；
(3)若存在x1、x2∈[－1，1]，使得|f(x1)－f(x2)|≥e－1，试求a的取值范围．
定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M>0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界．已知函数f(x)＝1＋a·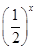
＋
.
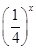(1)当a＝1时，求函数f(x)在(－∞，0)上的值域，并判断函数f(x)在(－∞，0)上是否为有界函数，请说明理由；
(2)若函数f(x)在[0，＋∞)上是以3为上界的有界函数，求实数a的取值范围．
已知f(x)＝xlnx，g(x)＝－x2＋ax－3.
(1)求函数f(x)在[t，t＋2](t>0)上的最小值；
(2)对一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求实数a的取值范围；
(3)证明对一切x∈(0，＋∞)，都有lnx>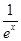
－
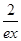成立．
设函数f(x)＝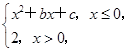
其中b>0，c∈R.当且仅当x＝－2时，函数f(x)取得最小值－2.
(1)求函数f(x)的表达式；
(2)若方程f(x)＝x＋a(a∈R)至少有两个不相同的实数根，求a取值的集合．