已知f(x)＝xlnx，g(x)＝－x2＋ax－3.
(1)求函数f(x)在[t，t＋2](t>0)上的最小值；
(2)对一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求实数a的取值范围；
(3)证明对一切x∈(0，＋∞)，都有lnx>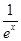
－
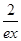成立．
（本小题满分12分）
据调查统计，通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数如下表：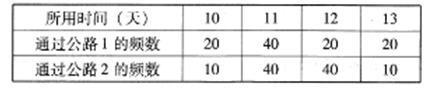
（Ⅰ）为进行某项研究，从所用时间为12天的60辆汽车中随机抽取6辆.
（ⅰ）若用分层抽样的方法抽取，求从通过公路1和公路2的汽车中各抽取几辆？
（ⅱ）若从（ⅰ）的条件下抽取的6辆汽车中，再任意抽取两辆汽车，求这两辆汽车至少有一辆通过公路1的概率？
（Ⅱ）假设汽车A只能在约定日期（某月某日）的前11天出发，汽车B只能在约定日期的前12天出发.为了尽最大可能在各自允许的时间内将货物运往城市乙，估计汽车A和汽车B应如何选择各自的路径？
(本小题满分12分)已知函数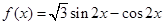
.
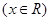（Ⅰ）求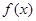
的单调递增区间；
（Ⅱ）在锐角三角形ABC中，a，b，c分别是角A，B，C的对边，若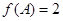
，
，
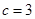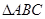的面积为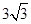
，求b的值.
（本小题满分10分）【选修4-5：不等式选讲】
已知函数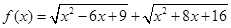
.
（Ⅰ）求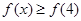
的解集；
（Ⅱ）设函数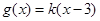
，
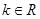，若
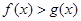对任意的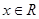
都成立，求实数k的取值范围.
（本小题满分10分）【选修4-4：坐标系与参数方程】
已知曲线C的极坐标方程为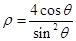
，以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，直线
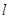的参数方程为
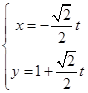（t为参数）.
（Ⅰ）把曲线C的极坐标方程化为直角坐标方程，把直线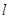的参数方程化为普通方程；
（Ⅱ）求直线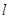被曲线C截得的线段AB的长.
（本小题满分10分）【选修4-1：几何证明选讲】
如图，已知直线PA与圆O相切于点A，经过点O的割线PBC交圆O于点B和点C，
的平分线分别交AB，AC于点D和E.
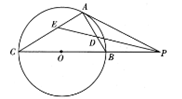
（Ⅰ）证明：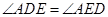
；
（Ⅱ）若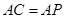
，求
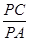的值.