已知:在梯形 中,
中, 点
点 是
是 的中点,
的中点, 是正三角形.动点P、Q分别在线段
是正三角形.动点P、Q分别在线段 和
和 上运动,且∠MPQ=60°保持不变.
上运动,且∠MPQ=60°保持不变.
(1)求证:△BMP∽△CPQ
(2)设PC= ,MQ=
,MQ= 求
求 与
与 的函数关系式;
的函数关系式;
(3)在(2)中,当 取最小值时,判断
取最小值时,判断 的形状,并说明理由.
的形状,并说明理由.
图是用10根火柴棒搭成的一个三角形,你能否移动其中的3根,摆出一对全等的三角形?画出你的修改方案.移动其中4根能否摆出一对全等三角形?请画图说明,并与同伴交流.
两块大小一样的含30°角的三角板,放在桌面上,可以拼出多种不同的图形.现在小红拼出了如图所示的四个图形,请你再动手拼一拼,至少再画出有别于小红这四个图形的四个不同图形,并与同伴交流.
为参加学校举行的风筝设计比赛,小明用四根竹棒扎成如图所示的风筝框架,已知AB=CD,AC=DB.你认为小明的风筝两脚的大小相同吗?(即∠B=∠C吗)试说明理由.
如图所示,AB=AD,BC=CD,AC、BD相交于点E,由这些条件你能推出哪些结论?(不再添加辅助线,不再标注其他字母,不写推理过程,只要求写出四个你认为正确的结论)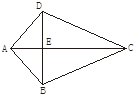
下面是4×4的正方形方格图形,如图所示.在A点有一只蚂蚁沿格线(虚线)爬行到B点,爬行路径正好把大正方形分割成全等的两个图形.请在图的a、b、c三个4×4正方形方格中分别画出三种不同的走法,把每个大正方形都分成两个全等图形.