如图，在坐标系中，菱形ABCD的边BC与x轴重合，点B与原点-优题课

题文

如图，在坐标系中，菱形ABCD的边BC与x轴重合，点B与原点重合，AB＝10， ∠ABC＝60°．动点P从点B出发沿BC边以每秒1个单位长的速度匀速运动；动点Q从点D出发沿折线DC－CB－BA以每秒3个单位长的速度匀速运动，过点P作PF⊥BC，交折线AB－AC于点E，交直线AD于点F．若P、Q两点同时出发，当其中一点到达终点时整个运动随之停止，设运动时间为t秒．
（1）写出点A与点D的坐标
（2）当t=3秒时，试判断QE与AB之间的位置关系？
（3）当Q在线段DC上运动时，若△PQF为等腰三角形，求t的值；
（4）设△PQE的面积为S，求S与t的函数关系式；

科目数学题型解答题难度较难

知识点：二次函数在给定区间上的最值

登录免费查看答案和解析

相关试题

先化简，再求值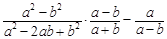：，其中，．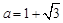

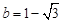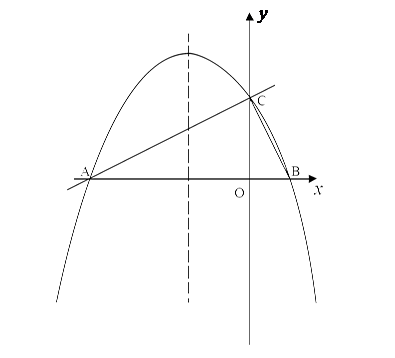
如图，在平面直角坐标系 $x O y$ 中，直线 $y = \frac{1}{2} x + 2$ 与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $C$ ．抛物线 $y = a x^{2} + b x + c$ 的对称轴是 $x = - \frac{3}{2}$ 且经过 $A$ 、 $C$ 两点，与 $x$ 轴的另一交点为点 $B$ ．

（1）①直接写出点 $B$ 的坐标；②求抛物线解析式．
（2）若点 $P$ 为直线 $A C$ 上方的抛物线上的一点，连接 $P A, P C$ ．求 $△ P A C$ 的面积的最大值，并求出此时点 $P$ 的坐标．
（3）抛物线上是否存在点 $M$ ，过点 $M$ 作 $M N$ 垂直 $x$ 轴于点 $N$ ，使得以点 $A$ 、 $M$ 、 $N$ 为顶点的三角形与 $△ A B C$ 相似？若存在，求出点 $M$ 的坐标；若不存在，请说明理由．

鄂州市化工材料经销公司购进一种化工原料若干千克，价格为每千克30元．物价部门规定其销售单价不高于每千克60元，不低于每千克30元．经市场调查发现：日销售量y（千克）是销售单价x（元）的一次函数，且当x=60时，y=80；x=50时，y=100．在销售过程中，每天还要支付其他费用450元．
（1）求出y与x的函数关系式，并写出自变量x的取值范围．
（2）求该公司销售该原料日获利w（元）与销售单价x（元）之间的函数关系式．
（3）当销售单价为多少元时，该公司日获利最大？最大获利是多少元？

如图，在△ABC中，AB=AC，AE是∠BAC的平分线，∠ABC的平分线 BM交AE于点M，点O在AB上，以点O为圆心，OB的长为半径的圆经过点M，交BC于点G，交 AB于点F．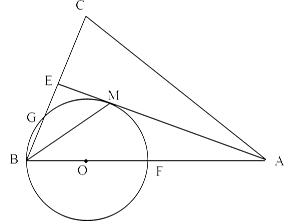

（1）求证：AE为⊙O的切线．
（2）当BC=8，AC=12时，求⊙O的半径．
（3）在（2）的条件下，求线段BG的长．

关于x的一元二次方程x²+（2k+1）x+k²+1=0有两个不等实根．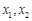
（1）求实数k的取值范围．
（2）若方程两实根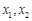满足｜x₁｜+｜x₂｜=x₁·x₂，求k的值．

试卷网试题网古诗词网作文网范文网