如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)求点D的坐标.
(2)求直线BC的解析式.
(3)在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
我市为改善农村生活条件,满足居民清洁能源的需求,计划为万宝村400户居民修建A、B两种型号的沼气池共24个.政府出资36万元,其余资金从各户筹集.两种沼气池的型号、修建费用、可供使用户数、占地面积如下表:
| 沼气池 |
修建费用(万元/个) |
可供使用户数(户/个) |
占地面积(平方米/个) |
| A型 |
3 |
20 |
10 |
| B型 |
2 |
15 |
8 |
政府土地部门只批给该村沼气池用地212平方米,设修建A型沼气池x个,修建两种沼气池共需费用y万元.
(1)求y与x之间函数关系式.
(2)试问有哪几种满足上述要求的修建方案.
(3)要想完成这项工程,每户居民平均至少应筹集多少钱?
已知△ABC中,M为BC的中点,直线m绕点A旋转,过B、M、C分别作BD⊥m于D,ME⊥m于E,CF⊥m于F.
(1)当直线m经过B点时,如图1,易证EM= CF.(不需证明)
CF.(不需证明)
(2)当直线m不经过B点,旋转到如图2、图3的位置时,线段BD、ME、CF之间有怎样的数量关系?请直接写出你的猜想,并选择一种情况加以证明.
一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地,两车同时出发.不久,第二列快车也从甲地发往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分后,第二列快车与慢车相遇.设慢车行驶的时间为x(单位:时),慢车与第一、第二列快车之间的距离y(单位:千米)与x(单位:时)之间的函数关系如图1、图2,根据图象信息解答下列问题:
(1)甲、乙两地之间的距离为 千米.
(2)求图1中线段CD所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接在图2中的( )内填上正确的数.
为了更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如下的调查问卷(单选).在随机调查了本市全部5000名司机中的部分司机后,整理相关数据并制作了右侧两个不完整的统计图:
克服酒驾﹣﹣你认为哪一种方式更好?
| A.司机酒驾,乘客有责,让乘客帮助监督 |
| B.在车上张贴“请勿喝酒”的提醒标志 |
| C.签订“永不酒驾”保证书 |
| D.希望交警加大检查力度 |
E.查出酒驾,追究就餐饭店的连带责任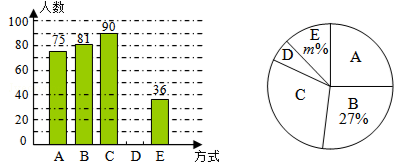
根据以上信息解答下列问题:
(1)请补全条形统计图,并直接写出扇形统计图中m= ;
(2)该市支持选项B的司机大约有多少人?
(3)若要从该市支持选项B的司机中随机抽取100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被抽中的概率是多少?