近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.
(1)求每台A种、B种设备各多少万元?
(2)根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
解不等式组: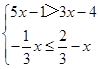 ,并用数轴把解集表示出来.
,并用数轴把解集表示出来.
如图,在平面直角坐标系中,抛物线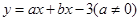 与x轴交于点A(-2,0),B(4,0)两点,与x轴交于点C。
与x轴交于点A(-2,0),B(4,0)两点,与x轴交于点C。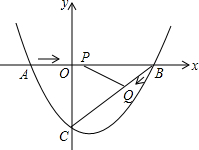
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使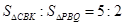 ,求K点坐标。
,求K点坐标。
我们知道平行四边形有很多性质。现在如果我们把平行四边形沿着它的一条对角线翻折。会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,∠B=30º, ,将△ABC沿AC翻折至
,将△ABC沿AC翻折至 ,连接
,连接 。
。
【发现与证明】:如图1:求证:①△AGC是等腰三角形;
② (只选一个证明哟,4分)
(只选一个证明哟,4分)
【应用与解答】:如图2:如果AB= ,BC=1,
,BC=1, 与CD相交于点E,求△AEC的面积
与CD相交于点E,求△AEC的面积
【拓展与探索】如果AB= ,当BC的长为多少时,△AB′D是直角三角形?
,当BC的长为多少时,△AB′D是直角三角形?
(阅读)如图1,在平面直角坐标系xoy中,已知点A(a、O)(a>0),B(2,3),C(0,3)。过原点O作直线l,使它经过第一、第三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
【理解】若点D与点A重合,则这个操作过程为FZ[,];直接写出答案
【尝试】
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;