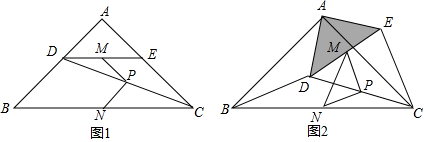
如图,已知直线 、
、 交于点
交于点 ,
,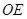 平分
平分 ,若
,若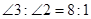 ,
,
求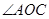 的度数.
的度数.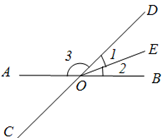
2018年5月13日清晨,我国第一艘自主研制的 型航空母舰从大连造船厂码头启航,赴相关海域执行海上试验任务已知舰长 约 ,航母前端点 到水平甲板 的距离 为 ,舰岛顶端 到 的距离是 ,经测量, , ,请计算舰岛 的高度.(结果精确到 ,参考数据: , , , , ,

某校七、八年级各有学生400人,为了解这两个年级普及安全教育的情况,进行了抽样调查,过程如下
选择样本,收集数据从七、八年级各随机抽取20名学生,进行安全教育考试,测试成绩(百分制)如下:
七年级 85 79 89 83 89 98 68 89 79 59
99 87 85 89 97 86 89 90 89 77
八年级 71 94 87 92 55 94 98 78 86 94
62 99 94 51 88 97 94 98 85 91
分组整理,描述数据
(1)按如下频数分布直方图整理、描述这两组样本数据,请补全八年级20名学生安全教育频数分布直方图;

解析数据,计算填空
(2)两组样本数据的平均数、中位数、众数、优秀率如下表所示,请补充完整;
|
年级 |
平均数 |
中位数 |
众数 |
优秀率 |
|
七年级 |
85.3 |
88 |
89 |
|
|
八年级 |
85.4 |
|
|
|
得出结论,说明理由.
(3)估计八年级成绩优秀的学生人数约为 人.
(4)整体成绩较好的年级为 ,理由为 (至少从两个不同的角度说明合理性).
如图,在 中, ,点 在 上,以线段 的长为半径的 与 相切于点 ,分别交 、 于点 、 ,连接 并延长,交 的延长线于点 .
(1)求证: .
(2)已知 的半径为3.
①若 ,则 .
②当 时,四边形 为菱形.

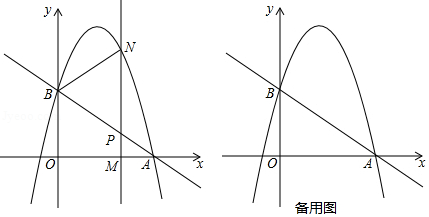
如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过点 , .
(1)求点 的坐标和抛物线的解析式;
(2) 为 轴上一动点,过点 且垂直于 轴的直线与直线 及抛物线分别交于点 , .
①点 在线段 上运动,若以 , , 为顶点的三角形与 相似,求点 的坐标;
②点 在 轴上自由运动,若三个点 , , 中恰有一点是其它两点所连线段的中点(三点重合除外),则称 , , 三点为“共谐点”.请直接写出使得 , , 三点成为“共谐点”的 的值.
如图1,在 中, , ,点 , 分别在边 , 上, ,连接 ,点 , , 分别为 , , 的中点.
(1)观察猜想:图1中,线段 与 的数量关系是 ,位置关系是 ;
(2)探究证明:把 绕点 逆时针方向旋转到图2的位置,连接 , , ,判断 的形状,并说明理由;
(3)拓展延伸:把 绕点 在平面内自由旋转,若 , ,请直接写出 面积的最大值.