如图①, 已知抛物线 (a≠0)与
(a≠0)与 轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
轴交于点A(1,0)和点B (-3,0),与y轴交于点C.
(1) 求抛物线的解析式;
(2) 点D的坐标为(-2,0).问:直线AC上是否存在点F,使得△ODF是等腰三角形?若存在,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
(3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求△BCE面积的最大值,并求此时E点的坐标.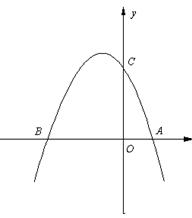
如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC折叠,使点B落在点E处,AE交CD于点F,连接DE.

(1)求证:△DEC≌△EDA;
(2)求DF的值;
(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其定点Q落在线段AE上,定点M、N落在线段AC上,求当线段PE的长为何值时,矩形PQMN的面积最大?
如图,已知⊙O上依次有A、B、C、D四个点, =
= ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
(1)若⊙O的半径为3,∠DAB=120°,求劣弧 的长;
的长;
(2)求证:BF= BD;
BD;
(3)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
2014年5月,我市某中学举行了“中国梦•校园好少年”演讲比赛活动,根据学生的成绩划分为A,B,C,D四个等级,绘制了不完整的两种统计图.
根据图中提供的信息,回答下列问题: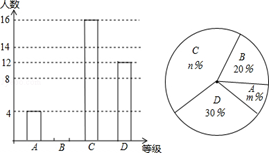
(1)参加演讲比赛的学生共有人,并把条形图补充完整;
(2)扇形统计图中,m=,n=;C等级对应扇形的圆心角为度;
(3)学校欲从获A等级的学生中随机选取2人,参加市举办的演讲比赛,请利用列表法或树形图法,求获A等级的小明参加市比赛的概率.
某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为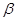 ,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为
,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为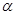 .测得A,B之间的距离为4米,
.测得A,B之间的距离为4米,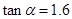 ,
,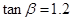 ,试求建筑物CD的高度.
,试求建筑物CD的高度.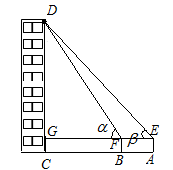
某漆器厂接到制作480件漆器的订单,为了尽快完成任务,该厂实际每天制作的件数比原来每天多50%,结果提前10天完成任务.原来每天制作多少件?