(本小题满分12分)甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为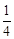 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为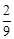 .
.
(Ⅰ)分别求甲、乙、丙三台机床各自加工的零件是一等品的概率;
(Ⅱ)若让每台机床各自加工2个零件(共计6个零件),求恰好有3个零件是一等品的概率.
(本小题满分12分)已知 ,动点
,动点 满足
满足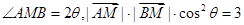 ,设
,设 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)过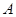 的直线
的直线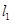 与曲线
与曲线 交于
交于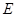 、
、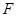 两点,过
两点,过 与
与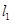 平行的直线
平行的直线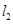 与曲线
与曲线 交于
交于 、
、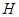 两点,求四边形
两点,求四边形 的面积的最大值.
的面积的最大值.
(本小题满分12分)如图,在三棱锥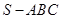 中,底面
中,底面 为直角三角形,且
为直角三角形,且 ,
,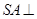 底面
底面 ,且
,且 ,点
,点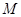 是
是 的中点,
的中点, 且交
且交 于点
于点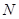 .
.
(1)求证: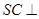 平面
平面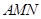 ;
;
(2)当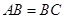 时,求二面角
时,求二面角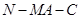 的余弦值.
的余弦值.
(本小题满分12分)某工厂生产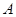 、
、 两种元件,某质量按测试指标划分,指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
两种元件,某质量按测试指标划分,指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
(1)试依据以频率估计概率的统计思想,分别估计元件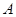 ,元件
,元件 为正品的概率;
为正品的概率;
(2)生产一件元件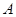 ,若是正品可盈利40元,若是次品则亏损5元;生产一件元件
,若是正品可盈利40元,若是次品则亏损5元;生产一件元件 ,若是正品可盈利50元,若是次品则亏损10元,在(1)的前提下:
,若是正品可盈利50元,若是次品则亏损10元,在(1)的前提下:
(i)记 为生产一件元件
为生产一件元件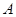 和1件元件
和1件元件 所得的总利润,求随机变量
所得的总利润,求随机变量 的分布列和数学期望;
的分布列和数学期望;
(ii)求生产5件元件 所获得的利润不少于140元的概率.
所获得的利润不少于140元的概率.
(本小题满分12分)已知各项均为正数的数列 的前
的前 项和为
项和为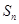 ,对任意
,对任意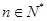 ,总有
,总有 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 的前
的前 项和
项和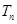 .
.
(本小题满分10)已知 .
.
(1)求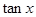 的值;
的值;
(2)求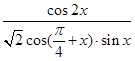 的值.
的值.