(本小题满分12分)已知 ,动点
,动点 满足
满足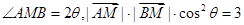 ,设
,设 的轨迹为曲线
的轨迹为曲线 .
.
(1)求曲线 的方程;
的方程;
(2)过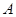 的直线
的直线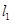 与曲线
与曲线 交于
交于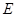 、
、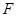 两点,过
两点,过 与
与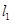 平行的直线
平行的直线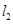 与曲线
与曲线 交于
交于 、
、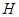 两点,求四边形
两点,求四边形 的面积的最大值.
的面积的最大值.
如图所示,一个半圆和长方形组成的铁皮,长方形的边 为半圆的直径,
为半圆的直径,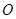 为半圆的圆心,
为半圆的圆心,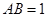 ,
,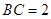 ,现要将此铁皮剪出一个三角形
,现要将此铁皮剪出一个三角形 ,使得
,使得 ,
, .
.
(1)设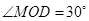 ,求三角形铁皮
,求三角形铁皮 的面积;
的面积;
(2)求剪下的铁皮三角形 的面积的最大值.
的面积的最大值.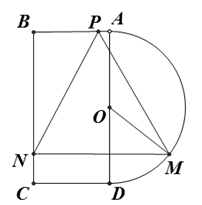
已知在锐角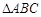 中,
中, 为角
为角 所对的边,且
所对的边,且 .
.
(1)求角 的值;
的值;
(2)若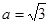 ,则求
,则求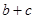 的取值范围.
的取值范围.
设等差数列 的前
的前 项和为
项和为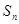 且
且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和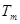 ,并求
,并求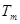 的最小值.
的最小值.
已知椭圆G: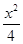 +y2=1.过
+y2=1.过 轴上的动点
轴上的动点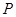 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(1)求椭圆G上的点到直线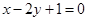 的最大距离;
的最大距离;
(2)①当实数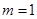 时,求A,B两点坐标;
时,求A,B两点坐标;
②将|AB|表示为m的函数,并求|AB|的最大值.
已知函数 (
( 是常数)在
是常数)在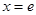 处的切线方程为
处的切线方程为 ,且
,且 .
.
(1)求常数 的值;
的值;
(2)若函数 (
( )在区间
)在区间 内不是单调函数,求实数
内不是单调函数,求实数 的取值范围.
的取值范围.